Electric Field Of A Dipole MCQ - Practice Questions with Answers

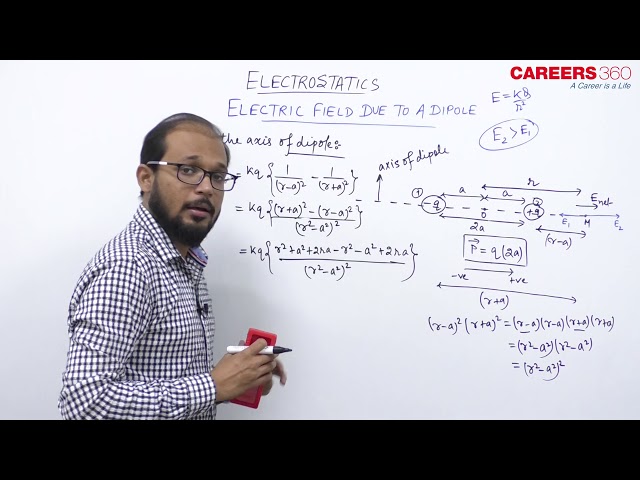
Electric Field Intensity due to an Electric Dipole at a Point on the Axial Line

As shown in the above figure We want to find out Electric Field Intensity due to an Electric Dipole at a Point M which is on axial line and at a distance r from the centre of a dipole.

Where $E_1$ and $E_2$ is the Electric Field Intensity at M due to $-q$ and $+q$ charges respectively.

The intensities $E_1$ and $E_2$ are along the same line but in opposite directions.

$
\begin{aligned}
& E_1=\frac{k q}{(r+a)^2} \\
& E_2=\frac{k q}{(r-a)^2} \\
& E_{\text {net }}=E_2-E_1
\end{aligned}
$

$
E_{n e t}=\frac{K q}{(r-a)^2}-\frac{K q}{(r+a)^2}=\left[\frac{4 \text { Kqar }}{\left(r^2-a^2\right)^2}\right]
$

Using $P=q(2 a)$

$
E_{\text {So }}=\left[\frac{4 K P r}{\left(r^2-a^2\right)^2}\right]
$

- For short/ldeal dipole (i.e r>>a)

then

$
\vec{E}_{n e t}=\frac{2 K \vec{P}}{r^3}=\frac{2 \vec{P}}{4 \pi \epsilon_0 r^3}
$

(This is the value of $E_{\text {net }}$ when the dipole is placed in the vacuum.)

If the dipole is placed in the medium having the permittivity as $\epsilon_m$

Then

$
\vec{E}_{n e t}=\frac{2 \vec{P}}{4 \pi \epsilon_m r^3}=\frac{2 \vec{P}}{4 \pi \epsilon_0 \epsilon_r r^3}
$

Note: The direction of the electric field E is in the direction of $\vec{P}$.
i.e Angle between $\mathrm{E}_{\mathrm{axi}}$ and $\vec{P}$ is $0^0$.

Electric Field Intensity due to an Electric Dipole at a Point on the Equitorial line.

As shown in the above figure We want to find out Electric Field Intensity due to an Electric Dipole at a Point M which is on the Equitorial line and at a distance r from the center of a dipole.

Where $E_1$ and $E_2$ is the Electric Field Intensity at M due to $-q$ and $+q$ charges respectively.

$
\begin{aligned}
& \left|\overrightarrow{E_1}\right|=\frac{1}{4 \pi \epsilon_0} * \frac{q}{r^2+a^2} \\
& \left|\overrightarrow{E_2}\right|=\frac{1}{4 \pi \epsilon_0} * \frac{q}{r^2+a^2} \\
& \text { so }\left|\overrightarrow{E_1}\right|=\left|\overrightarrow{E_2}\right|=|\vec{E}|
\end{aligned}
$

$
\begin{aligned}
|\vec{E}| & =2\left|E_1\right| \cos \theta \\
& =\frac{2}{4 \pi \epsilon_0} \cdot \frac{q}{\left(r^2+a^2\right)} \cos \theta \\
& =\frac{2}{4 \pi \epsilon_0} \cdot \frac{q}{\left(r^2+a^2\right)} \frac{a}{\sqrt{r^2+a^2}} \\
& =\frac{q \times 2 a}{4 \pi \epsilon_0\left(r^2+a^2\right)^{3 / 2}}
\end{aligned}
$

Using $P=q(2 a)$

$
\therefore \vec{E}=\frac{-\vec{P}}{4 \pi \epsilon_0\left(r^2+a^2\right)^{3 / 2}}
$

And
- For short/ldeal dipole (i.e r>>a)
then

$
\vec{E}_{n e t}=\frac{-K \vec{P}}{r^3}=\frac{-\vec{P}}{4 \pi \epsilon_0 r^3}
$

(This is the value of $E_{\text {net }}$ when the dipole is placed in the vacuum.)

If the dipole is placed in the medium having the permittivity as $\epsilon_m$

$
\text { Then } \vec{E}_{n e t}=\frac{-\vec{P}}{4 \pi \epsilon_m r^3}=\frac{-\vec{P}}{4 \pi \epsilon_0 \epsilon_r r^3}
$

Note: Here the direction of the electric field E is opposite to the direction of $\vec{P}$. i.e Angle between $\mathrm{E}_{\text {equi }}$ and $\vec{P}$ is $180^{\circ}$.