Electric Potential MCQ - Practice Questions with Answers

In an Electric field Electric potential V at a point, P is defined as negative of work done per unit charge in changing the position of test charge from some reference point to the given point.

Note-usually reference point is taken as infinity and potential at infinity is taken as Zero.

We know that

$
W=\int \vec{F} \cdot \overrightarrow{d r}
$

$
\text { So } V=-\frac{W}{q_0}=-\int \frac{\vec{F} \cdot \overrightarrow{d r}}{q_0}
$

$V \rightarrow$ Electric potential
The negative sign indicates that as the distance from the point increases, potential decreases.
- It is a scalar quantity.
-SI Unit $\rightarrow \frac{J}{C}=$ volt while CGS unit is stat volt

1 volt $=\frac{1}{300}$ stat volt.
- Dimension -

$
[V][V]=\left[\frac{W}{q_0}\right]=\left[\frac{M Q^2 T^{-2}}{A T}\right]=\left[M L^2 T^{-3} A^{-1}\right]
$
 

• Electric Potential at a distance 'r'

            If the Electric field is produced by a point charge q then 

$\begin{aligned} & F=\frac{K q q_0}{r^2} \\ & \qquad \begin{array}{l}V=-\frac{W}{q_0}=-\int \frac{\vec{F} \cdot \overrightarrow{d r}}{q_0} \\ \text { Using } \\ \qquad=-\frac{K q}{r} \\ \text { at } r=\infty \quad V=0=V_{\max }\end{array} \\ & \qquad \begin{array}{l} \\ V\end{array} \\ & \end{aligned}$

• Electric Potential difference

In the Electric field, the work done to move a unit charge from one position to the other is known as Electric Potential difference.

If the point charge Q is producing the field

Point A and B are shown in the figure.

=Electric potential at point A

=Electric potential at point B

$r_B \rightarrow$ the distance of charge at $B$
$r_A \rightarrow$ distance of charge at $A$
$\Delta V=$ The Electric potential difference in bringing charge q from point A to point B in the Electric field produced by Q .

$
\begin{aligned}
& \Delta V=V_B-V_A=\frac{W_{A \rightarrow B}}{q} \\
& \Delta V=-K Q\left[\frac{1}{r_B}-\frac{1}{r_A}\right]
\end{aligned}
$

- Superposition of Electric potential

The net Electric potential at a given point due to different point masses $\left(Q_1, Q_2, Q_3 \ldots\right)$ can be calculated by doing a scalar sum of their individuals Electric potential.

$
V=V_1+V_2+V_3+\cdots=\frac{k q_1}{r_1}+k \frac{q_2}{r_2}+\frac{k\left(-q_3\right)}{r_3}+\cdots=\frac{1}{4 \pi \varepsilon_0} \sum \frac{q_i}{r_i}
$
 

• Electric Potential due to Continious charge distribution

                  $V=\int d V=\int \frac{d q}{4 \pi \varepsilon_0 r}$

• Graphical representation

     As we move on the line joining two charges then the variation of Potential with distance is given below.

• Zero potential due to a system of a two-point charge

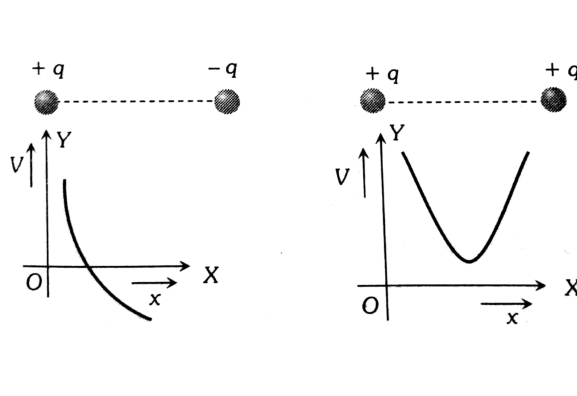
1.For internal point

(It is assumed that $\left|Q_1\right|<\left|Q_2\right|$ )
Let at $\mathrm{P}, \mathrm{V}$ is zero

$
\begin{aligned}
& V_P=0 \Rightarrow \frac{Q_1}{x_1}=\frac{Q_2}{\left(x-x_1\right)} \\
& \Rightarrow x_1=\frac{x}{\left(Q_2 / Q_1+1\right)}
\end{aligned}
$
 

If both charges are like then the resultant potential is not zero at any finite point.

2.For external point

Let at P, V is zero

$\begin{aligned} & V_P \Rightarrow \frac{Q_1}{x_1}=\frac{Q_2}{\left(x+x_1\right)} \\ & \Rightarrow x_1=\frac{x}{\left(Q_2 / Q_1-1\right)}\end{aligned}$