Virohan Allied & Healthcare Programs
Allied & Healthcare programs | 20+ Partner Universities & Institutes | 98% placement record
16 Questions around this concept.
If $E_a$ be the electric field strength of a short dipole at a point on its axial line and $E_e$ that on the equatorial line at the same distance, then
An electric dipole is placed along the $x$ - axis at the origin $O$. A point $P$ is at a distance of 20 from this origin such that OP makes an angle $\pi / 3$ with the $x$-axis. If the electric field at P makes an angle $\theta$ with the x-axis, the value of $\theta$ would be
An electric dipole of moment $\overrightarrow{\mathrm{p}}$ is placed at the origin along the x -axis. The angle made by the electric field with the $x$-axis at a point $P$, whose position vector makes an angle $\theta$ with the $x$-axis, is ( where $\tan \alpha=\frac{1}{2} \tan \theta$ )
NEET 2026: Application Form Link | Exam Centres List | How to Fill Form
NEET Prep: Mock Test | 10 Years PYQ's | Syllabus
NEET 2026: Boards Cheat Sheet | Mind Maps & Diagrams Guide | Formula Sheet
Latest: Allied and Health Sciences | Paramedical Universities Accepting Applications
A dipole is placed in an electric field as shown. In which direction will it move?
A point dipole $\vec{p}=-p_0 \hat{x} $ is kept at the origin. The potential and electric field due to this dipole on the $ \mathrm{y} \text {-axis at a }$ distance d are, respectively : ( Take $\mathrm{V}=0$ at infinity)
An electric dipole is placed as shown in the figure.

The electric potential (in $\left.10^2 \mathrm{~V}\right)$ at point P due to the dipole is $\left(\epsilon_0=\right.$ permittivity of free space and $\left.\frac{1}{4 \pi \epsilon_0}=K\right)$
Directions: Study the following line chart carefully and answer the questions given beside. Percent Profit earned by two companies producing electronic equipment from the year 2012 to 2017.
$ \text{Profit Percentage} = \left( \frac{\text{Profit}}{\text{Investment}} \right) \times 100 $
Profit = Revenue – Investment
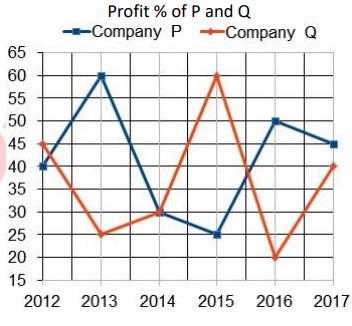
Company P invested Rs. 9,21,600 in the year 2018. The revenue of P in the year 2018 was equal to the revenue of Q in 2015 in which Q had invested Rs. 7.2 lakh. Find the profit percent of company P in the year 2018.
Allied & Healthcare programs | 20+ Partner Universities & Institutes | 98% placement record
Electric Potential due to an Electric Dipole at a Point on the Axial Line
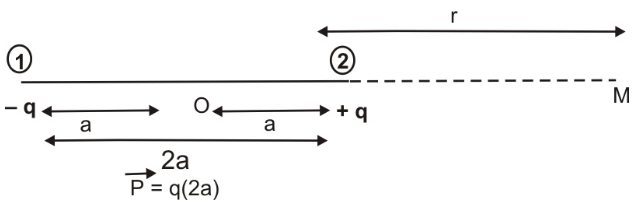
As shown in the above figure We want to find out Electric Potential due to an Electric Dipole at a Point M which is on axial line and at a distance r from the center of a dipole.
Where $V_1$ and $V_2$ is the Electric Potential at M due to $-q$ and $+q$ charges respectively.
$
\begin{aligned}
V_1 & =\frac{k q}{(r+a)} \\
V_2 & =\frac{k q}{(r-a)} \\
V_{\text {net }} & =V_2-V_1 \\
V_{\text {net }} & =V_1+V_2 \\
& =\frac{-k q}{(r+a)}+\frac{k_q}{(r-a)} \\
& =k_q\left\{\frac{1}{r-a}-\frac{1}{r+a}\right\} \\
& =k q\left\{\frac{(r+a)-(r-a)}{(r-a)(r+a)}\right\}
\end{aligned}
$
So $V_{n e t}=\frac{2 k q a}{r^2-a^2}$
Using $P=q(2 a)$
So $V_{\text {net }}=\frac{k P}{r^2-a^2}$
then
$
V_{n e t}=\frac{K P}{r^2}=\frac{P}{4 \pi \epsilon_0 r^2}
$
Electric potential due to an Electric Dipole at a Point on the Equitorial line.
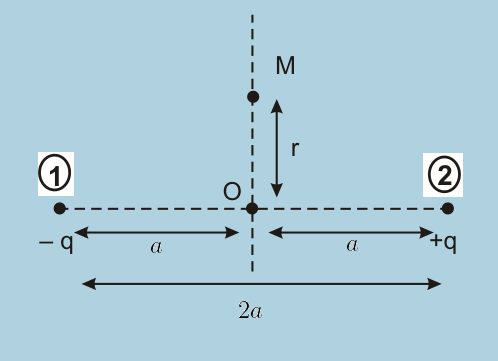
As shown in the above figure We want to find out Electric potential due to an Electric Dipole at a Point M which is on the Equitorial line and at a distance r from the center of a dipole.
Where $V_1$ and $V_2$ is the Electric Field Intensity at M due to $-q$ and $+q$ charges respectively.
$
\begin{aligned}
& V_1=-\frac{1}{4 \pi \epsilon_0} * \frac{q}{\sqrt{r^2+a^2}} \\
& V_2=\frac{1}{4 \pi \epsilon_0} * \frac{q}{\sqrt{r^2+a^2}} \\
& V_{\text {net }}=V_2-V_1=0
\end{aligned}
$
Electric potential due to a dipole at any general point-
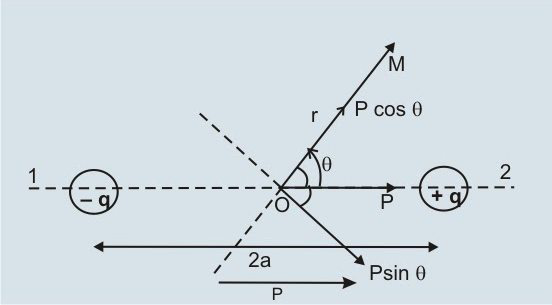
As shown in the above figure We want to find out Electric potential due to an Electric Dipole at a Point M which at a distance $r$ from the center of a dipole and making an angle $\theta$ with the axial line.
From the figure, M is at the axial line of dipole having dipole moment as $P \cos \theta$ and M is at the Equitorial line of dipole having dipole moment as $P \sin \theta$.
if $r \gg a$
$
\begin{aligned}
& V_a=\frac{1}{4 \pi \varepsilon_0} \times \frac{2 P \cos \theta}{r^2} \text { and } V_{\perp}=0 \\
& \text { then } \\
& \text { So } V_{\text {net }}=V_a=\frac{K P \cos \theta}{r^2}
\end{aligned}
$
"Stay in the loop. Receive exam news, study resources, and expert advice!"
