Potential Energy Of A Dipole In An Electric Field MCQ - Practice Questions with Answers

When a dipole is kept in a uniform electric field. The net force experienced by the dipole is zero as shown in the below figure.

I.e $F_{n e t}=0$

But it will experience torque. And Net torque about the center of dipole is given as

$
\tau=Q E d \sin \theta \text { or } \tau=P E \sin \theta \text { or } \vec{\tau}=\vec{P} \times \vec{E}
$

Work done in rotation-

Work done in rotation-

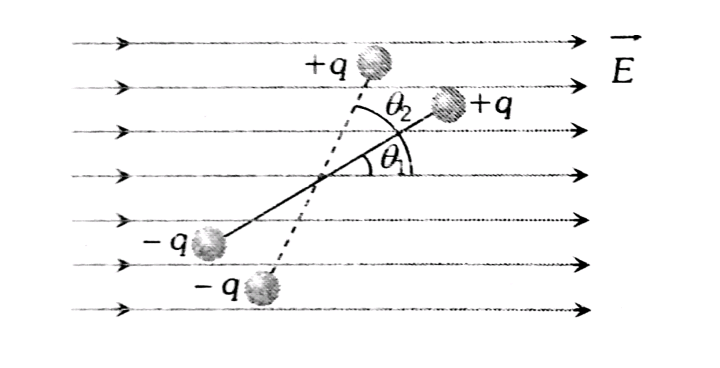
Then work done by electric force for rotating a dipole through an angle $\theta_2$ from the equilibrium position of an angle $\theta_1$ (As shown in the above figure) is given as

$
\begin{aligned}
& W_{\text {ele }}=\int \tau d \theta=\int_{\theta_1}^{\theta_2} \tau d \theta \cos \left(180^0\right)=-\int_{\theta_1}^{\theta_2} \tau d \theta \\
& \Rightarrow W_{\text {ele }}=-\int_{\theta_1}^{\theta_2}(P \times E) d \theta=-\int_{\theta_1}^{\theta_2}(P E \operatorname{Sin} \theta) d \theta=P E\left(\cos \Theta_2-\cos \Theta_1\right)
\end{aligned}
$

And So work done by an external force is $W=P E\left(\cos \Theta_1-\cos \Theta_2\right)$
For example

$
\begin{aligned}
& \text { if } \Theta_1=0^{\circ} \text { and } \Theta_2=\Theta \\
& W=P E(1-\cos \Theta) \\
& \text { if } \Theta_1=90^{\circ} \text { and } \Theta_2=\Theta \\
& W=-P E \cos \Theta
\end{aligned}
$

Potential Energy of a dipole kept in Electric field-

$
\text { As } \Delta U=-W_{\text {ele }}=W
$
 

So change in Potential Energy of a dipole when it is rotated through an angle $\theta_2$ from the equilibrium position of an angle $\theta_1$ is given as $\Delta U=P E\left(\cos \Theta_1-\cos \Theta_2\right)$

$
\begin{aligned}
& \text { if } \Theta_1=90^{\circ} \text { and } \Theta_2=\Theta \\
& \Delta U=U_{\theta_2}-U_{\theta_1}=U_\theta-U_{90}=-P E \cos \Theta
\end{aligned}
$

Assuming $\Theta_1=90^{\circ}$ and $U_{90^{\circ}}=0$
we can write $U=U_\theta=-\vec{P} \cdot \vec{E}$
Equilibrium of Dipole-
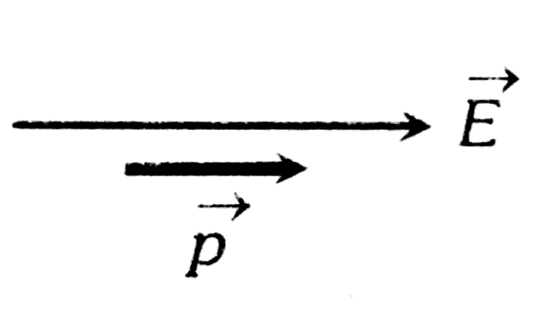
1. Stable Equilibrium-

$
\begin{aligned}
& \Theta=0^{\circ} \\
& \tau=0 \\
& U_{\min }=-P E
\end{aligned}
$
 

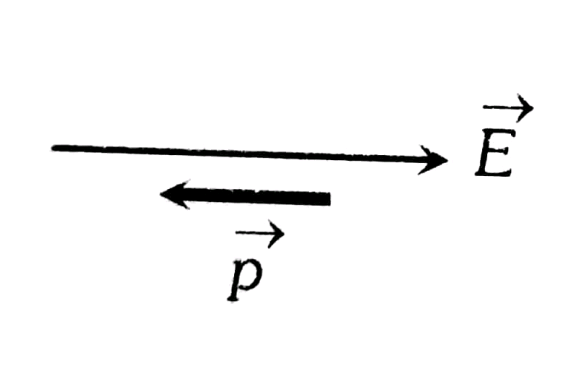
2. Unstable Equilibrium-

$\begin{aligned} & \Theta=180^{\circ} \\ & \tau=0 \\ & U_{\max }=P E\end{aligned}$

3. Not in equilibrium-

$\begin{aligned} & \Theta=90^{\circ} \\ & \tau_{\max }=P E \\ & U=0\end{aligned}$