Virohan Allied & Healthcare Programs
Allied & Healthcare programs | 20+ Partner Universities & Institutes | 98% placement record
12 Questions around this concept.
A progressive wave travelling along the positive x -direction is represented by $y(x, t)=A \sin (k x-w t+\phi)$. Its snapshot at $\mathrm{t}=0$ is given in the figure.

For this wave, the phase is :
The equation of a simple harmonic progressive wave is given by, Finding the distance between 2 particles having a phase difference of .
Two sound waves having a phase difference of 60° have a path difference of:
NEET 2026: Application Form Link | Exam Centres List | How to Fill Form
NEET Prep: Mock Test | 10 Years PYQ's | Syllabus
NEET 2026: Boards Cheat Sheet | Mind Maps & Diagrams Guide | Formula Sheet
Latest: Allied and Health Sciences | Paramedical Universities Accepting Applications
The equation of a wave is given by . If the displacement is 5cm at t=0, then the total phase at t = 7.5s is
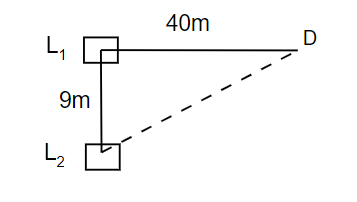
The loudspeakers and
driven. As the frequency of the oscillators increases from zero, the detector at D is recorded as a series of maximum and minimum signals. What is the frequency at which the first maximum is observed? (speed of sound
)
When the wave travels from a denser medium to rarer medium
In the equation , the term phase is defined as -
Allied & Healthcare programs | 20+ Partner Universities & Institutes | 98% placement record
The distance between two points differing in phase by on a wave having wave velocity
and frequency 500 Hz is
Equations of a stationary wave and a travelling wave are and
. The Phase difference between the two points
and
is
for the first wave and
for the second wave. The ratio
The general equation of sine wave is given as :
$$
y=A \sin (\omega t-k x+\phi)
$$
Here $\omega$, is the angular frequency i.e,
$$
\begin{aligned}
& \omega=\frac{2 \pi}{T}=2 \pi f_{\text {It defines how many cycles of the oscillations are there. }} \\
& \text { and } \phi=\text { phase angle. }
\end{aligned}
$$
Phase:
The quantity which expresses at any instant, the displacement of the particle and its direction of motion is called the phase of the particle.
If two particles of the medium, at any instant are in the same state of motion ( parameters such as the particle's displacement, velocity, and acceleration are same) then they are said to be in the same phase.
The phase of the wave is the quantity inside the brackets of the sin function, and it is an angle measured either in degrees or radians.
$$
\phi=\left(\frac{2 \pi}{T} t-\frac{2 \pi}{\lambda} x\right)
$$
At a particular time t . The phase difference of the wave between point $\mathrm{A}\left(x_1\right)$ and point $\mathrm{B}\left(x_2\right)$ is given by
$$
\begin{aligned}
\phi_1-\phi_2 & =\left(\frac{2 \pi}{\lambda} x_2-\frac{2 \pi}{\lambda} x_1\right) \\
\phi_1-\phi_2 & =\frac{2 \pi}{\lambda}\left(x_2-x_1\right)
\end{aligned}
$$
The important result here is that the two waves can be:Í
(1). In phase if $x_2-x_1=n \lambda$, i.e. the particles corresponding to positions $x_1$ and $x_2$ are in the same state of motion.
2) Out of phase if $x_2-x_1=\left(n+\frac{1}{2}\right) \lambda$ $x_{2 \text { is }}$ moving dowinwards but symmetrically.
"Stay in the loop. Receive exam news, study resources, and expert advice!"
