Force Between Two Parallel Current Carrying Conductors MCQ - Practice Questions with Answers

Force between two parallel current carrying infinite wires-

Let us take two long straight conductors carrying currents $i_{1 \text { and }} i_2$ placed parallel to each other at a distance 'a' from each other as shown in the figure -

Now, from the earlier concept which we have studied before, we can say that the conductor 2 experiences the some magnetic field at every point along its length due to the conductor 1. Because of this there will be some force acting on conductor 2 and the direction of magnetic force is indicated in the figure and it can be visualised by using the right-hand thumb rule. 

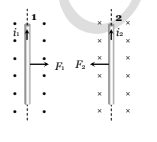
Now, if we apply Ampere's circuital law on the first conductor then the magnitude of the magnetic field can be obtained as -

$$
B_1=\frac{\mu_0 I_1}{2 \pi a}
$$

Then the force on a segment of length $L$ of the conductor 2 due to the conductor 1 can be given as,

$$
F_{21}=I_2 L B_1=\frac{\mu_0 I_1 I_2}{2 \pi a} L
$$

Similarly, we can calculate the force exerted by the conductor 2 on the conductor 1 . We see that, the conductor 1 experiences the same force due to the conductor 2 but the direction of force is opposite. Thus we can say that,

$$
F_{21}=F_{12} \quad \text { (But the direction will be opposite.) }
$$

But if the direction of current flowing through the conductor is opposite in both the conductors then both the wire will repel each other.
Also, the magnitude of force acting per unit length can be given as -

$$
f_{12}=f_{21}=\frac{\mu_0 I_1 I_2}{2 \pi a}
$$