Magnetic Field Due To Current In Straight Wire MCQ - Practice Questions with Answers
Quick Facts
-
Magnetic Field due to current in straight wire is considered one of the most asked concept.
-
38 Questions around this concept.
Solve by difficulty
The magnetic field at the origin due to the current flowing in the wire as shown in figure below is
Two identical conducting wires $A O B$ and $C O D$ are placed at right angles to each other. The wire $A O B$ carries an electric current $I_1$ and $C O D$ carries a current $I_2$. The magnetic field on a point lying at a distance $d$ from $O$, in a direction perpendicular to the plane of the wires $A O B$ and $C O D$, will be given by
In given fig. Magnetic Induction at the centre of the arc due to the current in portion AB will be

A long straight wire of radius carries a steady current I. The current is uniformly distributed over its cross-section. The ratio of the magnetic fields B and B', at radial distances $\frac{\text{a}} {2}$ and 2a respectively, from the axis of the wire is:
Two identical long conducting wires AOB and COD are placed at right angle to each other, with one above other such that 'O' is their common point for the two. The wires carry I1 and I2 currents, respectively. Point 'P' is lying at distance 'd' from 'O' along a direction perpendicular to the plane containing the wires. The magnetic field at the point 'P' will be :
Concepts Covered - 1
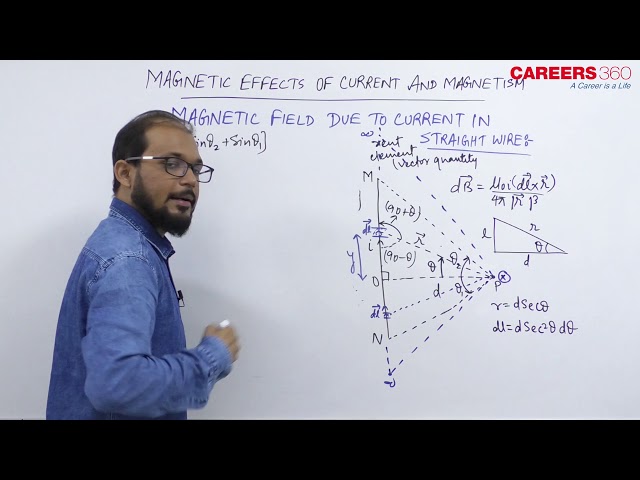
Magnetic Field due to current in straight wire:
Magnetic field lines around a current carrying straight wire are concentric circles whose centre lies on the wire.
Magnitude of magnetic field B, produced by straight current carrying wire at a given point is directly proportional to current I pairing through the wire i.e. $B \propto I . \mathrm{B}$ is inversely proportional to the distance 'r' from the /wire.
Magnetic field due to a current carrying wire at a point $P$ which lies at a perpendicular distance $r$ from the wire as shown is given as:
$$
B=\frac{\mu_0}{4 \pi} \cdot \frac{i}{r}\left(\sin \phi_1+\sin \phi_2\right)
$$
From figure, $\alpha=\left(90^{\circ}-\phi_1\right)$ and $\beta=\left(90^{\circ}+\phi_2\right)$
Hence,
$$
B=\frac{\mu_o}{4 \pi} \cdot \frac{i}{r}(\cos \alpha-\cos \beta)
$$

Different cases:
Case 1 : When the linear conductor XY is of finite length and the point P lies on it's perpendicular bisector as shown

$B=\frac{\mu_0}{4 \pi} \cdot \frac{i}{r}(2 \sin \phi)$
Case 2 : When the linear conductor XY is of infinite length and the point P lies near the centre of the conductor

$B=\frac{\mu_0}{4 \pi} \frac{i}{r}\left[\sin 90^{\circ}+\sin 90^{\circ}\right]=\frac{\mu_0}{4 \pi} \frac{2 i}{r}$
Case 3 : When the linear conductor is of infinite length and the point P lies near the end Y or X

$B=\frac{\mu_0}{4 \pi} \frac{i}{r}\left[\sin 90^{\circ}+\sin 0^{\circ}\right]=\frac{\mu_0}{4 \pi} \frac{i}{r}$
- When point P lies on axial position of current carrying conductor then magnetic field at P, B=0.
- The value of magnetic field induction at a point, on the centre of separation of two linear parallel conductors carrying equal currents in the same direction is zero.
- If direction of current in straight wire the known then direction of the magnetic field produced by straight wire carrying current is obtained by maxwell's right hand thumb rule.
Study it with Videos
"Stay in the loop. Receive exam news, study resources, and expert advice!"