Physical Pendulum MCQ - Practice Questions with Answers

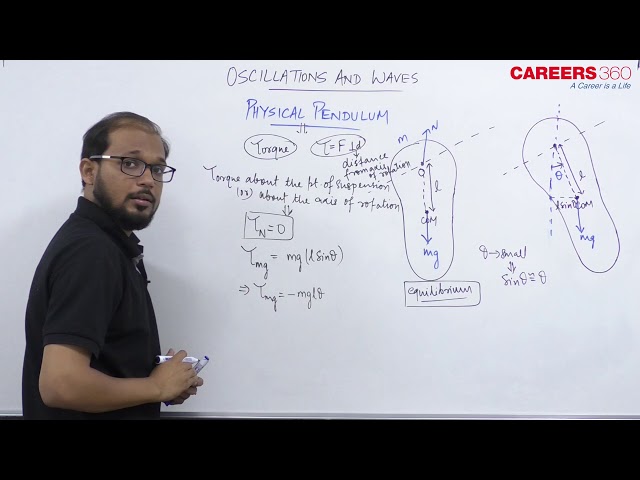
Physical pendulum- Any rigid body suspended from fixed support and can oscillate about that support then it is called a physical pendulum. e.g. A circular ring suspended on a nail in a wall etc.

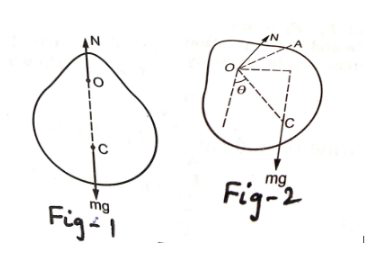
The body is in equilibrium, as shown in the above fig-1.

Now the body is displaced through a small angle $\theta$ as shown in the fig- 2 .
Let the distance between the point of suspension and center of mass of the body $=O C=l$
Then torque on the body about O is given by $\tau=m g l \sin \theta$
Now if $\mathrm{I}=$ moment of inertia of the body about O , Then $\tau=I \alpha$.
From the equation (1) and (2) we get

$$
\tau=I \alpha=I \frac{d \theta^2}{d t}=-m g l \sin \theta
$$

Since $\theta$ is very small so

$$
I \frac{d \theta^2}{d t}=-m g l \theta
$$

Comparing with the equation $\frac{d \theta^2}{d t}=-\omega^2 \theta$ we get

$$
\omega=\sqrt{\frac{m g l}{I}} \Rightarrow T=2 \pi \sqrt{\frac{I}{m g l}}
$$

Note-

Time peried, $T=2 \pi \sqrt{\frac{I}{m g l}} ; \quad I=I_{\mathrm{CM}}+m l^2$
Where $I_{C M}$ is moment of inertia relative to the axis which passes from the center of mass and parallel to the axis of oscillation.

$$
T=2 \pi \sqrt{\frac{I_{\mathrm{CM}}+\mathrm{m} l^2}{m g l}}, \text { where } \mathrm{I}_{\mathrm{CM}}=\mathrm{mk}^2
$$

$k$ is gyration radius (about an axis passing from center of mass)

$$
\begin{aligned}
T & =2 \pi \sqrt{\frac{m k^2+m l^2}{m g l}} \\
& =2 \pi \sqrt{\frac{k^2+l^2}{g l}}=2 \pi \sqrt{\frac{l_{\mathrm{eq}}}{g}} \\
L_{\mathrm{eg}} & =\frac{k^2}{l}+l=\text { cquivalent length of simple pendulum }
\end{aligned}
$$

 So the graph of the Time period (T) Vs length of a simple pendulum () is shown below

 $\begin{aligned} & T \text { is minimam when } l=k \\ \Rightarrow & T_{\min }=2 \pi \sqrt{\frac{2 k}{g}}\end{aligned}$