Relation Between Object And Image Velocity In Lens MCQ - Practice Questions with Answers

An object is kept at 40 cm from a concave mirror of a focal length 20 cm. If the object start moving perpendicular to the principle axis with 6 cm/s then the velocity of the image is :

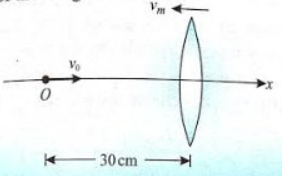
The velocity of a point is $v_0=2 \mathrm{~cm} / \mathrm{s}$ when it is placed at a distance of 30 cm from a lens moving with a speed $v_{\text {lens }}=2 \mathrm{~cm} / \mathrm{s}$ towards left. If the focal length of the lens is $f=20 \mathrm{~cm}$, find the velocity of the image.

A plane mirror is placed at origin parallel to y-axis facing the positive x-axis. An object starts from (2,0 ,0) with a velocity $(2 \hat{i}+2 \hat{j})$ m/s. The relative velocity of the image with respect to object is along:

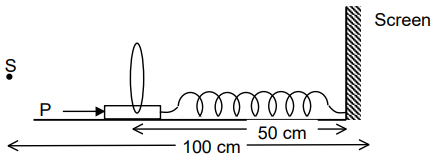
A point object is located at a distance of 100 m from a screen. A lens of focal length 23 cm mounted on a movable frictionless stand is kept between the source and the screen. The stand is attached to a spring of natural length 50cm and spring constant 800 N/m as shown. The mass of the stand with the lens is 2 kg. How much impulse P should be imparted to the stand so that a real image of the object is formed on the screen after a fixed time gap? (Neglect the width of the stand).

A man rowing his boat to cover a certain distance ‘X’. If the time taken by the man to cover the distance in upstream is 6 hours more than the time taken to cover the distance by the same boat in downstream. The speed of the stream is $37\frac {1}{2}\%$ of the speed of the boat in still water. If the man covers 110 km distance in downstream in 10 hours by the same boat, then find the value of ‘X’.