Silvering Of Lens MCQ - Practice Questions with Answers

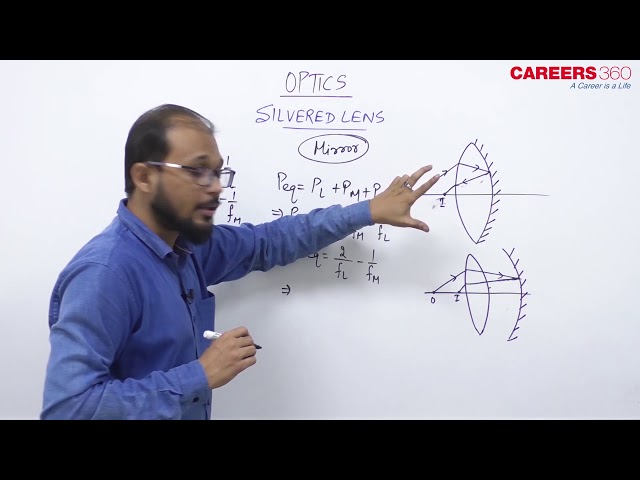
Silvered lens-

Silvering a surface has the effect of converting the lens into mirror.

As we have learned earlier that in a lens, a ray of light undergoes refraction and emerges on the side opposite to the side of the object. While in the case of a silvered lens, after refraction, a ray of light is reflected on the silvered surface and the ray emerges on the same side as the object.

If we silvered a convex lens, then that silvered side will act as concave mirror and similarly if we silvered the convex lens then the silvered side will act as a convex mirror. 

Our objective is to find the effective focal length of this silvered lens. Let us take an example of silvered convex lens as shown in the given figure.  

Now we use principle of superposition to find the focal length of the silvered lens. See the image given below which shows we are separating the lens and the mirror

See the image given below and see the arrangement. In this arrangement, a ray of light is first refraction by lens L, then it is reflected at the curved mirror M, and finally refracted once again at the lens L. Let the object O be located in front of the lens. Let the image from the lens  be formed at . 

Then, from the lens-makers formula, (Assume the focal length of the lens f_L1) we have

$$
\frac{1}{v_1}-\frac{1}{u}=\frac{1}{f_{L_1}}
$$

Now the image $\mathrm{I}_1$ formed by the lens will act as an object for the mirror having focal length $f_m$ Let $I_2$ be the image formed by the mirror at a distance of $\mathrm{v}_2$. Again applying the formula -

$$
\frac{1}{v_2}+\frac{1}{v_1}=\frac{1}{f_m}
$$

Now, $I_2$ will be the object for the final refraction at lens L. If $I_3$ be the final image formed at v from the center of the lens, then we

$$
\frac{1}{v}-\frac{1}{v_2}=\frac{1}{f_{L_2}}
$$

Now, $f_{L_1}=f_L \quad$ then $\quad f_{L_2}=f_L$

So the above equation become - 

$$
\begin{aligned}
& \frac{1}{v_1}-\frac{1}{u}=\frac{1}{f_L} \\
& \frac{1}{v_2}+\frac{1}{v_1}=\frac{1}{f_m} \\
& \frac{1}{v}-\frac{1}{v_2}=-\frac{1}{f_L}
\end{aligned}
$$

By manupulating the above equation we get,

$$
\frac{1}{v}+\frac{1}{u}=\frac{1}{f_m}-\frac{2}{f_L}
$$

So the equivalent focal length will be equal to -

$$
\frac{1}{f_e}=\frac{1}{f_m}-\frac{2}{f_L}
$$