Careers360 Logo
Medicine and Allied Sciences
Search Colleges, Exams, Schools & more
NEET 2024 Question Paper, Download Free PDF All SET Q, R, S, T Exam Paper
  1. Home
  2. NEET
  3. Study Material
  4. Centre Of Mass Of Semicircular Ring - Practice Questions & MCQ

Centre Of Mass Of Semicircular Ring - Practice Questions & MCQ

Edited By admin | Updated on Sep 25, 2023 25:23 PM | #NEET

Quick Facts

  • 3 Questions around this concept.

Concepts Covered - 1

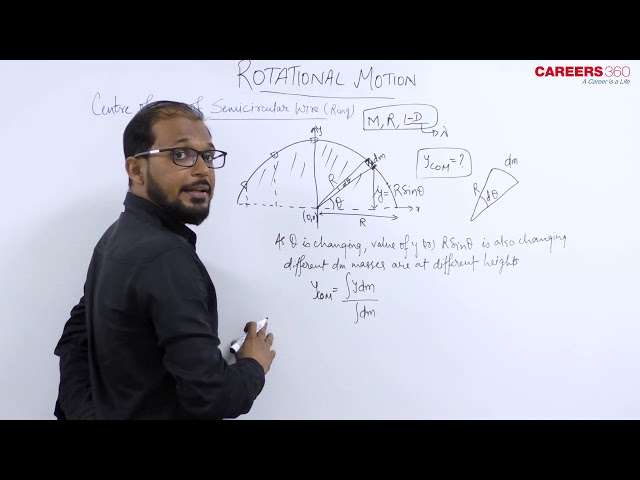
Position of centre of mass for semicircular ring

Have a look at the figure of semicircular ring.

 

Since it is symmetrical about y-axis on both sides of the origin

So we can say that  its x_{cm} = 0

And its z_{cm} = 0 as  z-coordinate is zero for all particles of semicircular ring.

Now, we will calculate its y_{cm} which is given by

y_{cm} = \frac{\int y.dm}{\int dm}

So , Take a small elemental arc of mass dm at an angle \theta  from the x-direction.

Its angular width d 

If the radius of the ring is R then its y coordinate will be Rsin

So,  dm=\frac{M}{\pi R}*Rd\theta =\frac{M}{\pi }d\theta

As,  y_{cm} = \frac{\int y.dm}{\int dm}

So, y_{cm}=\frac{\int_{\pi }^{0}\frac{M}{\pi R}*R*Rsin\theta d\theta}{M}=\frac{R}{\pi }\int_{\pi }^{0}sin\theta d\theta=\frac{2R}{\pi }

 

Study it with Videos

Position of centre of mass for semicircular ring

Study other Related Concepts

Centre Of Mass Of Semicircular Ring Current Topic

Rotational Motion Of Rigid Body
Center Of Mass
Center Of Mass Of The Uniform Rod
Centre Of Mass Of Semicircular Ring
Centre Of Mass Of Semicircular Disc
Centre Of Mass Of A Triangle
Centre Of Mass Of Hollow Hemisphere
Centre Of Mass Of Solid Hemisphere
Centre Of Mass Of Hollow Cone
Centre Of Mass Of A Solid Cone

"Stay in the loop. Receive exam news, study resources, and expert advice!"

Get Answer to all your questions

NEET Articles

NEET Exam Date 2024 (May 5): NEET Answer Key & Other Updates
May 18, 2024
NEET 2024 Latest News Updates - Admit Card, (Out), City Intimation (Released), Revised Syllabus
May 18, 2024
NEET Official Answer Key 2024, Download NEET UG Official Answer Key @exams.nta.ac.in
May 18, 2024
NEET 2024 Question Paper, Download Free PDF All SET Q, R, S, T Exam Paper
May 18, 2024
BDS Cut off For NEET 2024- Expected Cutoff For SC, OBC, ST, General
May 17, 2024
NEET 2024 - Answer Key (Out), Dates, Result, Cutoff Marks & Question Paper PDF
May 17, 2024
NEET Cut off 2023 - SC, OBC, ST, General For MBBS/BDS/BAMS Government & Private Colleges
May 17, 2024
NEET 2025 Syllabus PDF by NTA- NEET Subject-Wise New Syllabus PDF
May 17, 2024

Begin a career in Medical and Allied Sciences. Admissions Open for

ALLEN NEET Coaching
ALLEN NEET Coaching
Apply

Ace your NEET preparation with ALLEN Online Programs

Amrita Vishwa Vidyapeetham Allied & Life Science 2024
Amrita Vishwa Vidyapeetham Allied & Life Science 2024
Apply

Admissions Open for multiple allied and health sciences programs across 5 campuses | Ranked #7 in India by NIRF, NAAC A++ Accredited

Aakash Institute NEET Repeater
Aakash Institute NEET Repeater
Apply

Enroll for NEET 2025 preparation program- Class XII Passed Students

PW NEET Coaching
PW NEET Coaching
Apply

Enrol in PW Vidyapeeth center for NEET coaching

PACE IIT & Medical, Financial District, Hyd
PACE IIT & Medical, Financial District, Hyd
Apply

Enrol in PACE IIT & Medical, Financial District, Hyd for JEE/NEET preparation

NEET College Predictor
NEET College Predictor
Apply

Know possible Govt/Private MBBS/BDS Colleges based on your NEET rank

View All Application Forms
News and Notifications
May 06, 2024 - 12:16 PM IST :
May 06, 2024 - 12:15 PM IST :
May 05, 2024 - 07:15 AM IST :
NEET paper solver gang busted in Delhi, four held
May 18, 2024 - 09:59 PM IST
PIL in Patna HC seeks CBI probe into ‘NEET paper leak case’, cancellation of exam
May 18, 2024 - 12:03 PM IST
NEET UG 2024: SC refuses to stay result declaration over alleged paper leak
May 17, 2024 - 10:24 PM IST
NEET Cut-Off 2024: MBBS opening, closing ranks in Bihar medical colleges last year
May 16, 2024 - 06:51 PM IST
Free NEET counselling session by Careers360 on May 19
May 16, 2024 - 10:01 AM IST
Scrapping NEET only solution to stop student suicides, irregularities: Tamil Nadu's DMK
May 15, 2024 - 10:34 PM IST
NEET aspirant missing from Kota traced in Uttar Pradesh
May 14, 2024 - 07:33 PM IST

Download Careers360 App's

Regular exam updates, QnA, Predictors, College Applications & E-books now on your Mobile

  • student
    300M+

    Students

  • colleges
    36,000+

    Colleges

  • exams
    550+

    Exams

  • ebook
    1500+

    E-Books

  • certification
    16000+

    Certifications

student
Mobile Screen

We Appeared in

National Eligibility cum Entrance Test      
NEET Rank Predictor
Back to top