Medicine and Allied Sciences
Engineering and Architecture
Management and Business Administration
Law
Animation and Design
Media, Mass Communication and Journalism
Finance & Accounts
Computer Application and IT
Pharmacy
Hospitality and Tourism
Competition
School
Study Abroad
Arts, Commerce & Sciences
Learn
Online Courses and Certifications

NEET 2025 Latest News Updates By NTA: Exam Pattern, Syllabus & Mode

Home
NEET
Study Material
Elastic And Inelastic Collision MCQ - Practice Questions with Answers

Elastic And Inelastic Collision MCQ - Practice Questions with Answers

Edited By admin | Updated on Sep 25, 2023 25:23 PM | #NEET

Syllabus
Application Process
Exam Pattern
Admit Card
Preparation Tips
Result
Cutoff
Counselling Process
Answer Key
Mock Test
Exam Analysis
Question Paper
College Predictor
Eligibility Criteria
Dates
College Predictor
Rank Predictor
Accepting Colleges
Study Material

Quick Facts

Perfectly elastic oblique collision is considered one the most difficult concept.
Perfectly Elastic Head on Collision, Head on inelastic collision, Perfectly inelastic collision, Collision Between Bullet and Vertically Suspended Block is considered one of the most asked concept.
34 Questions around this concept.

Solve by difficulty

A block of mass 0.50 kg is moving with a speed of 2.00 ms^-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss (in Joule) during the collision is :

A

0.34 Joule

Correct Answer

Wrong Answer

B

0.16 Joule

Correct Answer

Wrong Answer

C

1 Joule

Correct Answer

Wrong Answer

D

0.67 Joule

Correct Answer

Wrong Answer

Two particles of masses m₁, m₂ move with initial velocities u₁ and u₂. On collision, one of the particles get excited to a higher level, after absorbing energy (E). If the final velocities of particles are v₁ and v₂ then we must have:

A

$m_1^{2}u_1 +m_2^{2}u_2 - E = m_1^{2}v_1 +m_2^{2}v_2$

Correct Answer

Wrong Answer

B

$\frac{1}{2}m_1u_1^{2}+ \frac{1}{2}m_2u_2^{2}= \frac{1}{2}m_1v_1^{2}+ \frac{1}{2}m_2v_2^{2}-E$

Correct Answer

Wrong Answer

C

$\frac{1}{2}m_1u_1^{2}+ \frac{1}{2}m_2u_2^{2}-E =\frac{1}{2}m_1v_1^{2}+ \frac{1}{2}m_2v_2^{2}$

Correct Answer

Wrong Answer

D

$\frac{1}{2}m_1u_1^{2}+ \frac{1}{2}m_2u_2^{2}+E =\frac{1}{2}m_1v_1^{2}+ \frac{1}{2}m_2v_2^{2}$

Correct Answer

Wrong Answer

A large number (n) of identical beads, each of mass m and radius r are strung on a thin smooth rigid horizontal rod of length L (L>>r) and are at rest at random positions. The rod is mounted between two rigid supports (see figure). If one of the beads is now given a speed $v$ , the average force experienced by each support after a long time is (assume all collisions are elastic) :

A

$\frac{mv^{2}}{L-nr}$

Correct Answer

Wrong Answer

B

$\frac{mv^{2}}{L-2nr}$

Correct Answer

Wrong Answer

C

$\frac{mv^{2}}{2\left ( L-nr \right )}$

Correct Answer

Wrong Answer

D

zero

Correct Answer

Wrong Answer

NEET 2024: Cutoff (OBC, SC, ST & General Category)

NEET 2024 Admission Guidance: Personalised | Study Abroad

NEET 2025: Syllabus | Most Scoring concepts | NEET PYQ's (2015-24)

NEET PYQ's & Solutions: Physics | Chemistry | Biology

Two identical balls A and B having velocities of 0.5 m/s and -0.3 m/s respectively collide elastically in one dimension. The velocities of B and A after the collision respectively will be:

A

-0.3 m/s and 0.5 m/s

Correct Answer

Wrong Answer

B

-0.5 m/s and 0.3 m/s

Correct Answer

Wrong Answer

C

0.3 m/s and 0.5 m/s

Correct Answer

Wrong Answer

D

0.5 m/s and -0.3 m/s

Correct Answer

Wrong Answer

Two particles A and B of equal mass M are moving with the same speed v as shown in the figure. They collide completely inelastically and move as a single particle C. The angle θ that the path of C makes with the X-axis is given by :

A

$\tan \Theta = \frac{\sqrt{3}+\sqrt{2}}{1-\sqrt{2}}$

Correct Answer

Wrong Answer

B

$\tan \Theta= \frac{\sqrt{3}-\sqrt{2}}{1-\sqrt{2}}$

Correct Answer

Wrong Answer

C

$\tan \Theta =\frac{1-\sqrt{2}}{\sqrt{2}\left ( 1+\sqrt{3} \right )}$

Correct Answer

Wrong Answer

D

$\tan \Theta =\frac{1-\sqrt{3}}{1+\sqrt{2}}$

Correct Answer

Wrong Answer

The question contains Statement-1 and Statement-2. Of the four choices given after the statements, choose the one that best describes the two statements.

Statement-1: Two particles moving in the same direction do not lose all their energy in a completely inelastic collision.

Statement-2: The principle of conservation of momentum holds true for all kinds of collisions.

A

Statement-1 is true, Statement-2 is false.

Correct Answer

Wrong Answer

B

Statement-1 is true, Statement-2 is true; Statement-2 is the correct explanation of Statement-1.

Correct Answer

Wrong Answer

C

Statement-1 is true, Statement-2 is true; Statement-2 is not the correct explanation of Statement-1.

Correct Answer

Wrong Answer

D

Statement-1 is false, Statement-2 is true.

Correct Answer

Wrong Answer

A mass m moves with a velocity $\nu$ and collides inelastically with another identical mass .After collision the first mass moves with velocity $\frac{v}{\sqrt{3}}$ in a direction perpendicular to the initial direction of motion.Find the speed of the 2^nd mass after collision

A

$\frac{2}{\sqrt{3}}v$

Correct Answer

Wrong Answer

B

$\frac{v}{\sqrt{3}}$

Correct Answer

Wrong Answer

C

$v$

Correct Answer

Wrong Answer

D

$3v$

Correct Answer

Wrong Answer

Pearson | PTE

Register now for PTE & Unlock 20% OFF : Use promo code: 'C360SPL20'. Valid till 31st DEC'24! Trusted by 3,500+ universities globally

Concepts Covered - 5

Perfectly Elastic Head on Collision

In Perfectly Elastic Collision,

Law of conservation of momentum and that of Kinetic Energy hold good.

$\frac{1}{2}m_{1}u_{1}^{2}+\frac{1}{2}m_{2}u_{2}^{2}= \frac{1}{2}m_{1}v_{1}^{2}+\frac{1}{2}m_{2}v_{2}^{2}$ …….(1)

$m_{1}u_{1}+m_{2}u_{2}=m_{1}v_{1}+m_{2}v_{2}$ …….(2)

$m_{1},m_{2}:masses$

$u_{1},v_{1}:initial \: and\: final \: velocity\: of \: the\: mass\ m_{1}$

$u_{2},v_{2}:initial \: and\: final \: velocity\: of \: the\: mass\ m_{2}$

From equation (1) and (2)

We get, $u_1-u_2 = v_2 - v_1$ …..(3)

Or, we can say Relative velocity of approach = Relative velocity of separation

And $e = \frac{v_2-v_1}{u_1-u_2} = \frac{Relative\ velocity\ of\ separation}{Relative\ velocity\ of\ approach}$

So in Perfectly Elastic Collision

e = 1 ,

From equations (1),(2), (3)

We get

$v_1 = (\frac{m_1-m_2}{m_1+m_2})u_1 + \frac{2m_2u_2}{m_1+m_2}$ ……(4)

Similarly, $v_2 = (\frac{m_2-m_1}{m_1+m_2})u_2 + \frac{2m_1u_1}{m_1+m_2}$ ...... (5)

Special cases of head on elastic collision

Equal mass in case of perfectly elastic collision

Then, $v_{1}= u_{2} \: and \: v_{2}= u_{1}$

Or, Velocity mutually interchange

If massive projectile collides with a light target (i.e $m_1>>m_2$ )

Since $m_1>>m_2$ so we use $m_2=0$

Putting $m_2=0$ in equation (4) and (5)

We get $v_1 = u_1\ and\ 2u_1-u_2$

If target particle is massive in case of elastic collision (i.e; $m_2>>m_1$ )

Since $m_2>>m_1$

So, the lighter particle recoil with same speed and the massive target particle remain practically at rest.

i.e; $\bar{v}_{2}=\bar u_2$

$\bar{v}_{1}=-\bar{u}_{1}$

Perfectly elastic oblique collision

Let two bodies moving as shown in figure.

By law of conservation of momentum

Along x-axis-

$m_1u_1+m_2u_2 = m_1v_1cos\theta+m_2v_2cos\phi$ ….. (1)

Along y-axis-

$0 = m_1v_1sin\theta-m_2v_2sin\phi$ …..(2)

By law of conservation of kinetic energy

$\frac{1}{2}m_{1}u_{1}^{2}+\frac{1}{2}m_{2}u_{2}^{2}= \frac{1}{2}m_{1}v_{1}^{2}+\frac{1}{2}m_{2}v_{2}^{2}$ ….(3)

And In Perfectly Elastic Oblique Collision

Value of e=1

So along line of impact (here along in the direction of $v_2$ )

We apply e=1

And we get $e=1=\frac{v_2-v_1cos(\theta+\phi)}{u_1cos\phi-u_2cos\phi}$ ….. (4)

So we solve these equations (1),(2),(3),(4) to get unknown.

Special condition

$if\ m_1 = m_2\ and\ u_2 = 0$

Then, from equation (1), (2) and (3)

We get, $\theta+\phi=\frac{\pi }{2}$

i.e; after perfectly elastic oblique collision of two bodies of equal masses (if the second body is at rest), the scattering angle $\theta+\phi$ would be $90^{0}$ .

Head on inelastic collision

In Inelastic Collision Law of conservation of momentum hold good but kinetic energy is not conserved .

$\frac{1}{2}m_{1}u_{1}^{2}+\frac{1}{2}m_{2}u_{2}^{2}\neq \frac{1}{2}m_{1}v_{1}^{2}+\frac{1}{2}m_{2}v_{2}^{2}$

$m_{1}u_{1}+m_{2}u_{2}= m_{1}v_{1}+m_{2}v_2$ …… (1)

$m_{1},m_{2}: masses$

$u_{1},v_{1}: initial \: and \: final\: velocities\: of \: mass \: m_{1}$

$u_{2},v_{2}: initial \: and \: final\: velocities\: of \: mass \: m_{2}$

In inelastic collision (0 < e < 1)

$e = \frac{v_2-v_1}{u_1-u_2}$ ….. (2)

From equations (1),(2)

We get,

$v_1 = (\frac{m_1-em_2}{m_1+m_2})u_1+\frac{(1+e)m_2}{m_1+m_2}u_2$ ……(3)

Similarly, $v_2 = (\frac{m_2-em_1}{m_1+m_2})u_2+\frac{(1+e)m_1}{m_1+m_2}u_1$ ...... (4)

Special case

A sphere of mass m moving with velocity u hits inelastically with another stationary sphere of same mass.

As, $e = \frac{v_2-v_1}{u_1-u_2}$

So, $e = \frac{v_2-v_1}{u}$ or, $ue = v_2-v_1$ ....(5)

By conservation of momentum

As, $m_{1}u_{1}+m_{2}u_{2}= m_{1}v_{1}+m_{2}$

So $v_2+v_1 = u$ ….(6)

From equation (5) and (6)

We get, $\frac{v_1}{v_2} = \frac{1-e}{1+e}$

Loss in kinetic energy

Loss in K.E = Total initial kinetic energy – Total final kinetic energy

$\bigtriangleup K.E. = (\frac{1}{2}m_1u^2_1+\frac{1}{2}m_2u^2_2)-(\frac{1}{2}m_1v^2_1+\frac{1}{2}m_2v^2_2)$ …. (7)

From equation (3) , (4) and (7)

We can write, Loss in kinetic energy in terms of e as

$\bigtriangleup K.E. = \frac{1}{2}(\frac{m_1m_2}{m_1+m_2})(1-e^2)(u_1-u_2)^2$

Perfectly inelastic collision

In Perfectly Inelastic Collision - Two bodies stick together after the collision ,so there will be a final common velocity (v)

When the colliding bodies are moving in the same direction

By the law of conservation of momentum

$m_1u_1+m_2u_2=(m_1+m_2)v$

$v=\frac{m_1u_1+m_2u_2}{(m_1+m_2)}$

Loss in kinetic energy

$\begin{aligned} \Delta K . E &=\left(\frac{1}{2} m_{1} u_{1}^{2}+\frac{1}{2} m_{2} u_{2}^{2}\right)-\left(\frac{1}{2}\left(m_{1}+m_{2}\right) V^{2}\right) \\ \Delta K . E &=\frac{1}{2}\left(\frac{m_{1} m_{2}}{m_{1}+m_{2}}\right)\left(u_{1}-u_{2}\right)^{2} \end{aligned}$

When the colliding bodies are moving in the opposite direction

By the law of conservation of momentum

$\\ {m_{1} u_{1}+m_{2}\left(-u_{2}\right)=\left(m_{1}+m_{2}\right) v} \\ \\ {v=\frac{m_{1} u_{1}-m_{2} u_{2}}{m_{1}+m_{2}}}$

If v is positive then the combined body will move along the direction of motion of mass $m_1$

If v is negative then the combined body will move in a direction opposite to the motion of mass $m_1$

Loss in kinetic energy

$\\ {\Delta K . E=\left(\frac{1}{2} m_{1} u_{1}^{2}+\frac{1}{2} m_{2} u_{2}^{2}\right)-\left(\frac{1}{2}\left(m_{1}+m_{2}\right) V^{2}\right)} \\ \\ {\Delta K . E=\frac{1}{2}\left(\frac{m_{1} m_{2}}{m_{1}+m_{2}}\right)\left(u_{1}+u_{2}\right)^{2}}$

Collision Between Bullet and Vertically Suspended Block

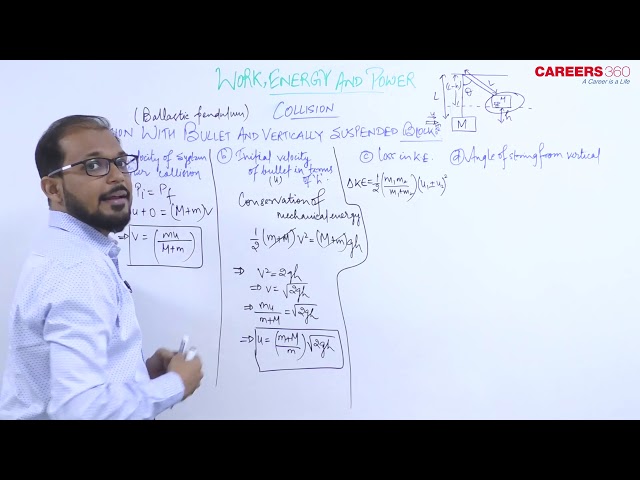
A block of mass M suspended by vertical thread.

A bullet of mass m is fired horizontally with velocity u in the block.

Let after the collision bullet gets embedded in block.

And, the combined system raised upto height h where the string makes an angle $\theta$ with the vertical.

Common velocity of system just after the collision (V)

Here, system is (block + bullet)

$\\ {\text { P=momentum }} \\ \\ {P_{\text {bullet}}+P_{\text {block}}=P_{\text {system}}} \\ \\ {m u+0=(m+M) V} \\\\ {V=\frac{m u}{m+M}}$ .....(1)

Initial velocity of the bullet in terms of h

By the conservation of mechanical energy

$\\ {(T . E \text { of system }) \text { Just after collision }=(T . E \text { of system) At height } h} \\\\ {\frac{1}{2}(m+M) V^{2}=(m+M) g h} \\ \\ {V=\sqrt{2 g h}} \\ \\ {\text { Equating }(1) \text { and }(2)} \\ \\ {\text { We get } V=\sqrt{2 g h}=\frac{m u}{m+M}}$

$u=\left(\frac{m+M}{m}\right) \sqrt{2 g h}$

Loss in kinetic energy

Loss of kinetic energy in perfectly inelastic collision when $(u_2=0 )$ is given by

$\Delta K . E=\frac{1}{2}\left(\frac{m M}{m+M}\right) u^{2}$

Value of angle $\theta$

$\\ {\text { From } u=\left(\frac{m+M}{m}\right) \sqrt{2 g h}} \\\\ {\text { We can write }} \\\\ {h=\left(\frac{u^{2}}{2 g}\right)\left(\frac{m}{m+M}\right)^{2}} \\\\{\text { And from figure }} \\\\ Or,\ {\cos \theta=\frac{L-h}{L}=1-\frac{h}{L}=1-\left(\left(\frac{u^{2}}{2 g L}\right)\left(\frac{m}{m+M}\right)^{2}\right)}$

Study it with Videos

Perfectly Elastic Head on Collision

Perfectly elastic oblique collision

Head on inelastic collision

Perfectly inelastic collision

Collision Between Bullet and Vertically Suspended Block

Study other Related Concepts

Elastic And Inelastic Collision Current Topic

Work Done By A Constant Force

Work Done By Variable Force

Conservative And Non-conservative Forces

Basics Of Energy And Its Various Forms

Potential Energy

Law Of Conservation Of Energy

Vertical Circular Motion

"Stay in the loop. Receive exam news, study resources, and expert advice!"

Get Answer to all your questions

NEET Articles

NEET Deleted Syllabus 2025 - NEET Reduced Syllabus Subject-wise

Dec 12, 2024

AFMS PG Medical Admission 2024 - Round 2 Registration (Started), Counselling, Merit List

Dec 12, 2024

How Many Days Left for NEET 2025? - Countdown NEET 2025

Dec 12, 2024

NEET Qualification Criteria 2025 by NTA - 12th Marks PDF, Percentage, Nationality

Dec 12, 2024

NEET Syllabus 2025 PDF by NTA- Download Subject-Wise Syllabus

Dec 12, 2024

AP NEET Merit List 2024 (Out)- Download Final Merit List at ntruhs.ap.nic.in

Dec 12, 2024

AP NEET Application Form 2024 (Extended For Management Quota)- Fees, How to Fill

Dec 12, 2024

Will NEET 2025 be Postponed? - Latest Updates Here

Dec 12, 2024

Quick Facts
Practice Questions
Concept Covered
Concept Video

Begin a career in Medical and Allied Sciences. Admissions Open for

NEET College Predictor

Know possible Govt/Private MBBS/BDS Colleges based on your NEET rank

NEET Companion

Register for Careers360 NEET Counseling & Admission Guidance Service.

TOEFL ® Registrations 2024

Accepted by more than 11,000 universities in over 150 countries worldwide

Manav Rachna-MRIIRS Allied Health Sciences Admissions 2025

Admissions open for Bachelor of Physiotherapy, B.Sc Nutrition & Dietetics ,B.Sc Food Science & Technology

View All Application Forms

News and Notifications

Max Healthcare Foundation launches Max Medical Scholarship programme for 100 MBBS Students

December 11, 2024 - 02:51 PM IST

NEET UG 2025 exam date soon; know cut-off for MBBS in top government medical colleges

December 04, 2024 - 08:06 PM IST

MP AYUSH NEET UG 2024 stray vacancy choice-filling ends today; reporting from December 6

December 03, 2024 - 10:26 PM IST

Maharashtra NEET UG Counselling: HC asks medical college to admit student denied MBBS seat in fee row

December 03, 2024 - 06:47 PM IST

NEET 2025 exam date soon; top medical colleges in India

November 30, 2024 - 02:52 PM IST

MP AYUSH NEET UG Counselling 2024: Stray vacancy round 3 merit list today, choice filling begins December 2

November 29, 2024 - 11:22 AM IST

AACCC AYUSH UG 2024: Special stray vacancy round choice filling deadline today; allotment on November 29

November 27, 2024 - 04:01 PM IST

Explore on Careers360

NEET

NEET Application Form

NEET Admit card

NEET Syllabus

NEET Answer Key

NEET Cutoff

NEET Result

NEET Exam Dates

NEET Counselling

RPVT

RPVT Application Form

RPVT Admit Card

RPVT Answer Key

RPVT Result

RPVT Seats

RPVT Syllabus

AIIMS Nursing

AIIMS Nursing Application Form

AIIMS Nursing Admit Card

AIIMS Nursing Result

Indian Army BSc Nursing

Indian Army BSc Nursing Application Form

Indian Army BSc Nursing Admit Card

Indian Army BSc Nursing Model Question Paper

Indian Army BSc Nursing Result

By Degree

Top M.B.B.S. Colleges in India

Top B.Sc. Colleges in India

Top B.D.S. Colleges in India

By Branch

Top Pathology Colleges in India

Top Gynaecology and Obstetrics Colleges in India

Top General Medicine and Surgery Colleges in India

Top General Nursing and Midwifery Colleges in India

By Exam

Medical Colleges in India Accepting NEET

By City

Top Medical Colleges in Bangalore

Top Medical Colleges in Chennai

Top Medical Colleges in Kolkata

Top Medical Colleges in Pune

Top Medical Colleges in Mumbai

Top Medical Colleges in New Delhi

Top Medical Colleges in Hyderabad

Top Medical Colleges in Ahmedabad

By State

Top Medical Colleges in Maharashtra

Top Medical Colleges in Karnataka

Top Medical Colleges in Tamilnadu

Top Medical Colleges in Punjab

Top Medical Colleges in Uttar Pradesh

Top Medical Colleges in Rajasthan

Top Medical Colleges in Madhya Pradesh

Top Medical Colleges in Gujarat

Top Medical Colleges in West Bengal

Download Careers360 App

All this at the convenience of your phone

Regular Exam Updates
Best College Recommendations
College & Rank predictors
Detailed Books and Sample Papers
Question and Answers

Scan and download the app

OR

About
Hiring
Magazine
News
Contact
Blogs

Medical Colleges in India
Private Medical Colleges in India
Government Medical Colleges in India
Government Medical Colleges in Uttar Pradesh
Medical Colleges in Tamil Nadu
Medical Colleges in Maharashtra
Medical Colleges in Karnataka
Medical Colleges in Kerala
Medical Colleges in Bihar
Medical Colleges in West Bengal
Medical Colleges in Haryana
AIIMS Delhi
CMC Vellore

NEET 2025
NEET MDS Exam
NEET PG 2024
FMGE 2024
INI CET 2025 January Session
AIAPGET 2024
NEET SS 2024
DNB PDCET 2024
AIIMS Bsc Nursing Exam
AIAPGET 2024

NEET Rank Predictor
NEET PG Rank Predictor
NEET College Predictor
NEET PG College Predictor
DNB CET College Predictor
DNB PDCET College Predictor
NEET MDS College Predictor
Medical E-books
Medical Sample Papers
NEET E-Books
Download NEET Sample Papers

NEET Exam
NEET Counselling 2024
NEET PG Counselling 2024
NEET Cut off
NEET Study Material 2025
NEET Online Preparation
Popular Medical Branches
QnA - Get answers to your doubts
Download App
Counselling Webinars
Online Certification Courses
NEET Question Papers
NEET 2025 Exam Date

Sitemap
Disclaimer
Comment Policy
Privacy Policy
Grievance Redressal

Copyright © 2024 Pathfinder Publishing Pvt Ltd.

National Eligibility cum Entrance Test

NEET 2025 Syllabus

Back to top