MEDIUMPearson | PTE
Trusted by 3,500+ universities and colleges globally | Accepted for migration visa applications to AUS, CAN, New Zealand , and the UK
Rigid Bodies: Translational Motion And Rotational Motion MCQ - Practice Questions with Answers
Edited By admin | Updated on Sep 25, 2023 25:23 PM | #NEET
Quick Facts
-
14 Questions around this concept.
Solve by difficulty
A solid sphere and cylinder of identical radii and mass approach an incline with the same liner velocity (see figure ). Both roll without slipping all throughout. The two climb maximum heights $h_{s p h}$ and $h_{c y l}$ on the incline. The ratio $\frac{h_{s p h}}{h_{c y l}}$ is given by:
As given in the diagram two plates A and B move with velocities -V and 3V . If the sphere does not slide relative to the plate . Assuming mass of each body as m Find the kinetic energy of sphere
A hollow sphere rolling on a surface. what is the of its translational kinetic energy -
NEET 2025: Syllabus | Most Scoring concepts | NEET PYQ's (2015-24)
A solid sphere is rolling on a surface its speed is and mass
.The its Kinetic energy is__
A heavy spool of inner radius ' ' and outer radius '
' is lying on a rough horizontal plane. Thread of negligible mass is wound over it and is being pulled with a constant force at an angle '
' from the vertical as shown in the figure. Find the angle '
' for which the centre of the spool remains at rest.
As shown in figure a particle of mass m moves in the x - y plane with a velocity v along the direction AB. $L_A$ is the angular momentum of a particle at A with respect to origin and $L_B$ when it is at B then
Two balls of mass and
are suspended on two strings of length
and
at the end of a freely hanging rod.
The rod is rotating with an angular velocity of about the vertical axle such that it remains in the vertical position. If the tension in the strings are
and
respectively, then find the sum of
and
.
A rod with linear mass density given, as -
where, is the distance from its left most end and '
' is the length of the rod. If the rod is placed on a smooth horizontal plane and a force of constant magnitude
is applied on its rightmost end then the angular acceleration of the rod will be.
Two hollow cylinders of radii ' ' and '
' respectively have common geometrical aixs as shown in the figure.
A fly starts with a constant speed ' ' and hits the outer cylinder at ' X ' from inside. If both the cylinder starts rotating with an angular velocity of '
'. The fly strikes another point ' Y ' where the distance between ' X ' and ' Y ' is
. Assuming the fly moves radially, find the speed of the fly.
Most Scoring concepts for NEET
This ebook serves as a valuable study guide for NEET exams, specifically designed to assist students in light of recent changes and the removal of certain topics from the NEET exam.
Download EBookA rope is wrapped around the rim of a wheel of moment of inertia 0.10 Kg-m2 and radius 10 cm. The wheel is fixed such that it can freely rotate about its axis. If a person is pulling the rope with the constant force of 10 N. Find the length of the rope detached from the pulley for t=0 to t=10 s
Concepts Covered - 2
Combined rotation and translation motion
-
Pure Translational motion-
If each particle of it has same velocity/acceleration at a particular instant of time then A body is said to have pure translational motion.
-
Slipping-
It is motion in which the body slides on a surface without rotation.
Example- Motion of a wheel on a frictionless surface.
Here friction between the body and surface =f= 0
Wheel possess only translatory kinetic energy
i.e., -
-
Pure rotational motion-
When a body rotates such that its axis of rotation does not move then that body is said to have pure rotational motion.
In pure rotational motion each particle of body has same angular velocity/acceleration about its axis of rotation at a particular instant of time.
Example- Spinning of wheel about fixed axis
Here axis of rotation of a wheel is fixed.
Here body possess only rotary kinetic energy.
I.e
Here Rotational angular momentum =
Where = Moment of inertia about fixed axis of rotation
= angular velocity of rotation
Another example- Motion of blades of a fan
-
Combined rotation and translation motion
In this type of motion body is having both rotation and translation motion.
-
Rolling
In case of rolling motion a body rotates about a fixed axis, and the axis of rotation also moves.
Example- Rolling of football on ground
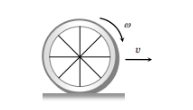
Here friction between the body and surface =
-
Kinetic energy-
Total kinetic energy of body is sum of both translational and rotational kinetic energy.
Using
- Net Velocity at a point-
Where,
Angular momentum in case of Combined rotation and translation motion
Angular momentum is always calculated about a particular point.
Net Angular momentum of body is sum of angular momentum due to both translational and rotational motion.
Where represents the angular momentum of the body about center of mass and r is the position vector about which we have to calculate the angular momentum.
Study it with Videos
Combined rotation and translation motion
Angular momentum in case of Combined rotation and translation motion"Stay in the loop. Receive exam news, study resources, and expert advice!"
Get Answer to all your questions
NEET Articles
Jan 20, 2025
Back to top