MEDIUMPearson | PTE
Register now for PTE & Unlock 20% OFF : Use promo code: 'C360SPL20'. Valid till 31st DEC'24! Trusted by 3,500+ universities globally
Variation Of Pressure MCQ - Practice Questions with Answers
Edited By admin | Updated on Sep 25, 2023 25:23 PM | #NEET
Quick Facts
-
Variation of pressure is considered one of the most asked concept.
-
27 Questions around this concept.
Solve by difficulty
A U tube with both ends open to the atmosphere, is partially filled with water. Oil, which is immiscible with water, is poured into one side until it stands at a distance of 10 mm above the water level on the other side. Meanwhile the water rises by 65 mm from its original level (see diagram). The density of the oil is
Water stands at a height H in a tall cylinder (see Fig)
. Two holes A and B are made on the sides of the cylinder. If hole A is at a height h above the ground, what is the height of hole B above the ground so that the two streams of water emerging from holes A and B strike the ground at the same point?
A large block of ice thick has a vertical hole drilled through it and is floating in the middle of a lake. The minimum length of the rope required to scoop up bucket full of water through the hole is (the relative density of ice
)
NEET 2024: Cutoff (OBC, SC, ST & General Category)
NEET 2024 Admission Guidance: Personalised | Study Abroad
NEET 2025: Syllabus | Most Scoring concepts | NEET PYQ's (2015-24)
If a rubber cube is taken deep in a lake, its volume is reduced by
The bulk modulus of rubber is nearly.
A bucket contains water filled up to a height . The bucket is tied to a rope which is passed over a frictionless light pulley and the other end of the rope is tied to a weight of mass that is half of that of the (bucket + water). The water pressure above the atmosphere pressure at the bottom is
A fire hydrant delivers water of density at a volume rate
. The water travels vertically upward through the hydrant and then does
turn to emerge horizontally at speed V. The pipe and nozzle have uniform cross-section throughout. The force exerted by the water on the corner of the hydrant is :
A hemispherical portion of radius is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass is M. It is suspended by a string in a liquid of density
where it stays vertical. The upper surface of the cylinder is at a depth h below the liquid surface. The force on the bottom of the cylinder by the liquid is
A tank is filled with water up to a height Water is allowed to come out of a hole P in one of the walls at a depth D below the surface of water. Express the horizontal distance
in terms of
and D
A cylindrical vessel contains a liquid of density \rho upto a height h. The liquid is dosed by a piston of mass m and area of cross-section
A. There is a small hole at the bottom of the vessel. The speed v with which the liquid comes out of the holes :
Most Scoring concepts for NEET
This ebook serves as a valuable study guide for NEET exams, specifically designed to assist students in light of recent changes and the removal of certain topics from the NEET exam.
Download EBookA body floats in a liquid with one-fourth volume out of liquid. The same body floats in water with its one-third volume out of water. Find the density of the liquid.
Concepts Covered - 1
Variation of pressure
-
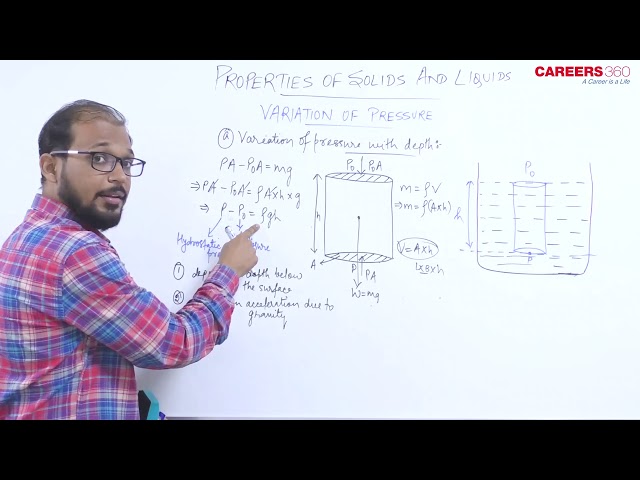
Variation of pressure with depth
-
Pressure varies with height/depth
Have a look at the below figure
Here P0= Atmospheric pressure at the upper surface
And h= depth below the upper surface
= density of liquid
P=Hydrostatic pressure for a point at depth h below the upper surface
Then P is given by
Means Pressure increases with depth linearly.
i.e. rate of increase of pressure with depth
-
Hydrostatic pressure=Absolute Pressure=
Absolute Pressure is always positive, It can never be zero.
From equation
We can say that
-
Hydrostatic pressure depends on
-
h=depth of the point below the surface
-
=nature of liquid
-
g=acceleration due to gravity
-
Hydrostatic pressure does not depend on
-
amount of liquid
-
the shape of the container
From this, we can say that for the below figure where the liquid is filled in vessels of
different shapes to the same height,
the pressure at the base in each vessels will be the same, though
the volume or weight of the liquid in different vessels will be different.
I.e In the above figure
-
Gauge Pressure- Gauge Pressure is known as the pressure difference between hydrostatic and atmospheric pressure.
So Gauge Pressure is given as
In the equation
The term is known as pressure due to liquid column of height h
We can rewrite the above equation as
Or we can say that Gauge Pressure =
It may be positive or negative or zero
-
Variation of pressure along Horizontally
The pressure is uniform on a horizontal line.
For the below figure
In horizontal line or in horizontal plane in stationary liquid
Study it with Videos
Variation of pressure"Stay in the loop. Receive exam news, study resources, and expert advice!"
Books
Reference Books
Clear your Basics with NCERT
E-books & Sample Papers
Get Answer to all your questions
NEET Articles
Back to top