The National Eligibility Cum Entrance Test (NEET) Paper has questions from Physics, Chemistry and Biology. The weight of Physics is 25% of total marks. As NEET is highly competitive, each subject is important. Most of the NEET students find Physics difficult. But enough practice and clarity in concepts can make Physics easy for students. Each chapter of the Physics syllabus for NEET is important. Here is the analysis of the Class 12 chapter Alternating Current and explanations on concepts and questions of the topic, Alternating Current, the LCR circuits.

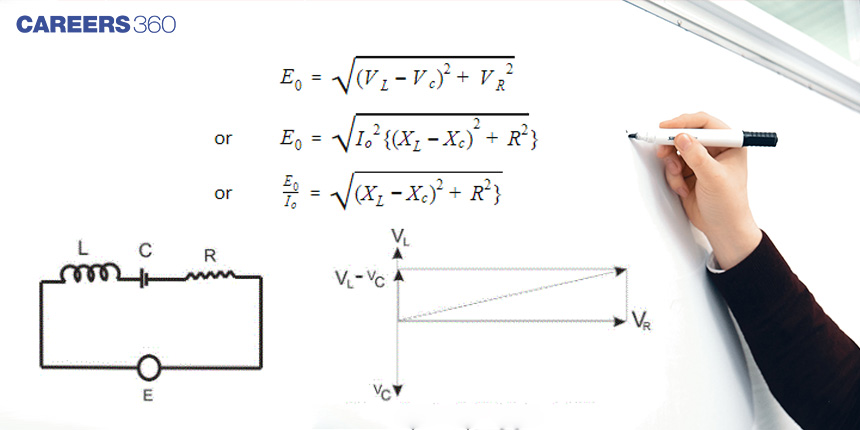
NEET Previous Year Papers’ Analysis: LCR Circuits, Concepts And Solutions

LCR Circuit(Image: Shutterstock)

In the last six years' paper of NEET there were 8 questions from AC circuits and out of these five questions were associated with the series LCR circuit. There were two questions from AC circuits in NEET 2021 in which one question was of LCR series circuit and another a combination of the concept of LCR circuit and series resonance. It shows that AC circuits and the concepts of LCR series circuits are important for NEET examination. JEE Main also has a number of questions from the LCR circuits. Let us have a look at the LCR series circuit.

LCR Series Circuit

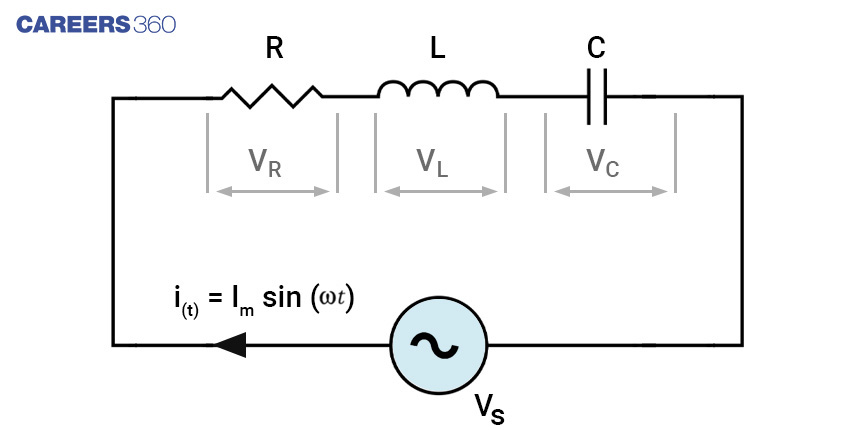
1653630750417

R, L and C are connected in series across an ac voltage source. The current may lead or lag the voltage depending on the values of resistance and inductive and capacitive reactance by some angle ɸ. The calculation of ɸ is discussed later.

Force Voltage Analogy

Applying Kirchoff's voltage Law to the given RLC series circuit we get

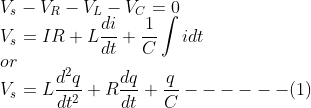
$\\V_s-V_R-V_L-V_C=0\\V_s=IR+L\frac{di}{dt}+\frac{1}{C}\int idt\\or\\V_s=L\frac{d^2q}{dt^2}+R\frac{dq}{dt}+\frac{q}{C}------(1)$

The equation of damped or forced oscillator(Studied in the chapter, Oscillation of Class 11) is

$F=m\frac{d^2x}{dt^2}+B\frac{dx}{dt}+Kx------(2)$

Comparing (1) and (2) the inductance L is analogous to mass m, resistance R is analogous to frictional coefficient B and capacitance is analogous to the 1/K where K is the spring constant.

Force Voltage Analogy

Mechanical Quantity	Electrical Quantity
Force	Voltage
Velocity	Current
Displacement	Charge
frictional coefficient	Resistance
Mass	Inductance
Spring constant	1/Capacitance

Question (JEE Main 2020)

A LCR circuit behaves like a damped harmonic oscillator. Comparing it with a physical spring-mass damped oscillator having damping constant 'b', the correct equivalence would be?

$L\leftrightarrow k,C\leftrightarrow b,R\leftrightarrow m$
$L\leftrightarrow m,C\leftrightarrow k,R\leftrightarrow b$
$L\leftrightarrow m,C\leftrightarrow \frac{1}{k},R\leftrightarrow b$
$L\leftrightarrow \frac{1}{b},C\leftrightarrow \frac{1}{m},R\leftrightarrow \frac{1}{k}$

JSS University Mysore 2025

NAAC A+ Accredited| Ranked #24 in University Category by NIRF | Applications open for multiple UG & PG Programs

Apply

Virohan Allied & Healthcare Programs

Allied & Healthcare programs | 20+ Partner Universities & Institutes | 98% placement record

Apply

Option c) is the right answer.

Phasor Diagram Of Series RLC Circuit

Phasor diagram for V_L>V_C

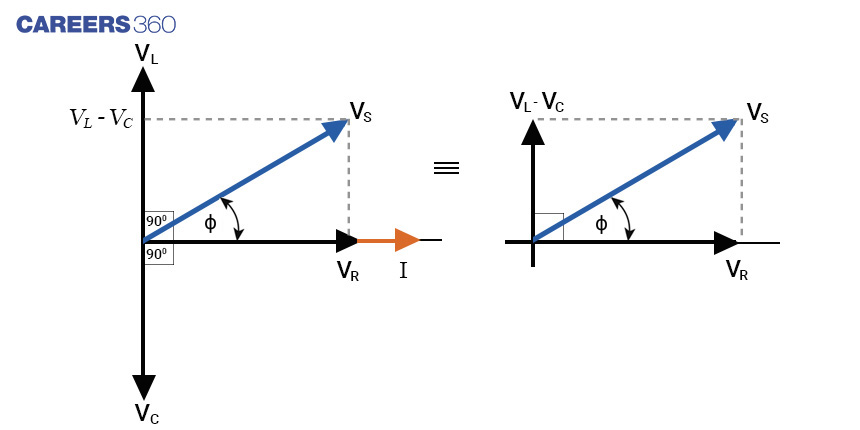
1653630753171

Phasor diagram for V_C>V_L

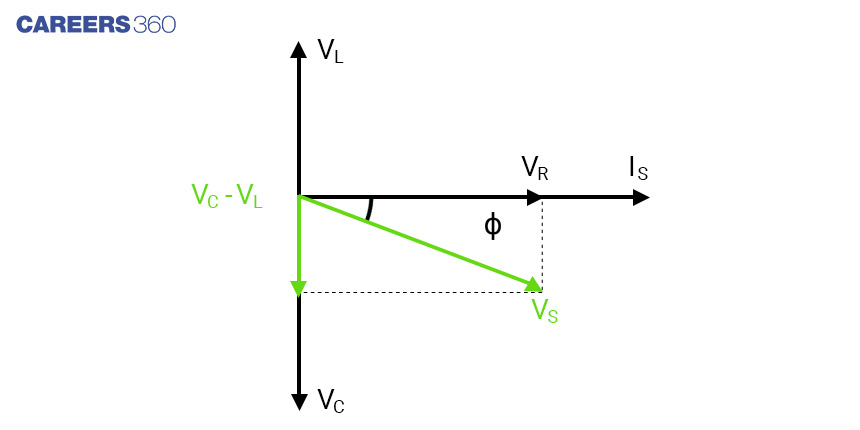
1653630754041

ɸ is the phase difference(angle between the resultant voltage and the current)

Resultant Voltage Of LCR Series Circuit

Question (JEE Main 2014)

When the RMS voltages V_L, V_C and V_R are measured respectively across the inductor L, the capacitor C and the resistor R in a series LCR circuit connected to an AC source, it is found that the ratio V_L: V_C: V_R = 1:2:3. If the RMS voltage of the AC source is 100 V, then V_R (in V) is close to

Solution:

$\\Given\\100=\sqrt{V_R^2+(V_L-V_C)^2}$

From the given ratio

$\\V_C=\frac{2}{3}V_R\ And \ V_L=\frac{1}{3}V_R$

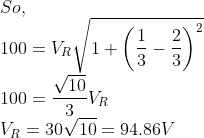
$\\So,\\100=V_R\sqrt{1+\left ( \frac{1}{3}-\frac{2}{3} \right )^2}\\100=\frac{\sqrt{10}}{3}V_R\\V_R=30\sqrt{10}=94.86V$

Recommended eBooks

Related eBooks & Sample Papers

Top 20 Multi-Concept Questions for NEET Physics 2026 with Detailed Solutions (PDF)

637+ Downloads

Top 75 Most Repeated NEET Chemistry Questions for 2026 (PYQ-Based) – Free PDF

671+ Downloads

Impedance Z Of LCR Series Circuit

$Z=\sqrt{R^2+(X_L-X_C)^2}$

As X_L=⍵L and X_C=1/(⍵C), the impedance can be calculated as

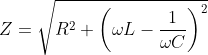
$Z=\sqrt{R^2+\left (\omega L-\frac{1}{\omega C}\right )^2}$

Impedance Triangle

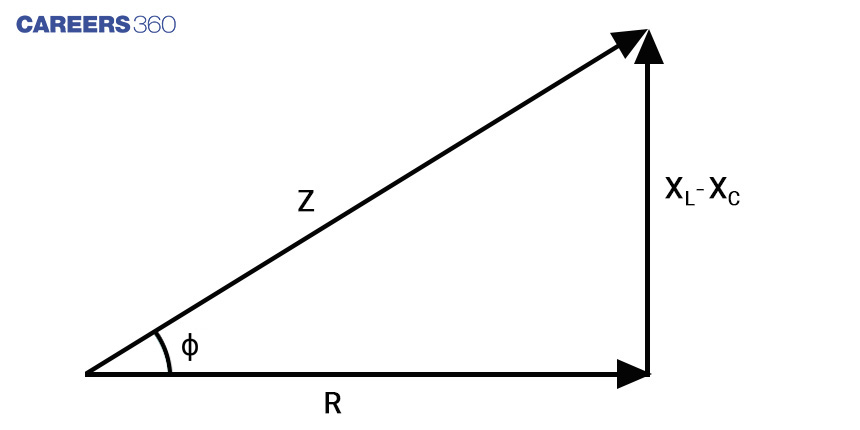
1653630749757

From the impedance triangle the angle phi can be calculated using trigonometric functions.

That is cosɸ=R/Z and cosɸ is known as the power factor.

$tan\phi=\frac{|X_L-X_C|}{R}$

$sin\phi=\frac{|X_L-X_C|}{Z}$

Question(JEE Main 2017)

A sinusoidal voltage of peak value 283 V and angular frequency (⍵) as 320 rad/s is applied to a series LCR circuit. Given that R=5 Ω, L=25 mH and C=1000 µF. The total impedance and phase difference between the voltage across the source and the current will be:

Solution:

Impedance

$Z=\sqrt{R^2+(X_L-X_C)^2}$

$X_{L} =\omega L = (2\pi f) L = 320\times25\times 10^{-3}\Omega=8\Omega$

$X_{C} = \frac{1}{\omega C} = \frac{1}{320\times10^{-3}} \Omega = \frac{1}{0.32}\Omega=3.125\Omega$

$Z=\sqrt{5^2+(8-3.125)^2}=6.98\Omega$

The phase difference between the voltage across the source and the current

$\phi=cos^{-1}\frac{R}{Z}=cos^{-1}\frac{5}{6.98}\approx 45^0$

NEET Syllabus: Subjects & Chapters

Select your preferred subject to view the chapters

Power In An AC Circuit

Instantaneous Power

It is the product of instantaneous voltage and current. That is:

$\\p=V_msinwtI_msin(wt-\phi)\\$

Using the trigonometric relation

$sinasinb=\frac{1}{2}(cos(a-b)-cos(a+b))$

$p=\frac{1}{2}V_mI_m(cos\phi-cos(2wt-\phi))$

Average Power

Voltage and current are not constant in an AC circuit, they change with respect to time. So power also changes. So the average power over a period T is

$\\P_{avg}=\frac{1}{T}\int_{0}^{T}vidt$

Where vi is the instantaneous power

$\\P_{avg}=\frac{1}{T}\int_{0}^{T}vidt$

$\\P_{avg}=\frac{1}{T}\int_{0}^{T}\frac{1}{2}V_mI_m[cos\phi-cos(2wt-\phi)]dt\\\int_{0}^{T}cos(2wt-\phi)dt=0\\So\ P_{avg}=\frac{V_mI_m}{2}cos\phi\\ P_{avg}=\frac{V_m}{\sqrt{2}}\frac{I_m}{\sqrt{2}}cos\phi=V_{rms}I_{rms}cos\phi$

Where cosɸ is known as the power factor.

Average power is measured in Watts. Average power is also known as active power or true power.

Also, average power can be written as

$\\P_{avg}=apparent \ power\times cos\phi$

Apparent power is measured in VA(Volt Ampere)

Power Factor

The power factor cosɸ can be calculated as-

$cos\phi=\frac{Average \ power}{Apparent\ power}$

Cosɸ can also be calculated from impedance triangle. Refer to the impedance triangle discussed above.

Reactive Power (Wattless Power)

$Reactive\ Power=V_{rms}I_{rms}sin\phi$

Reactive power is measured in VAr (Volt Ampere reactive)

Power Triangle

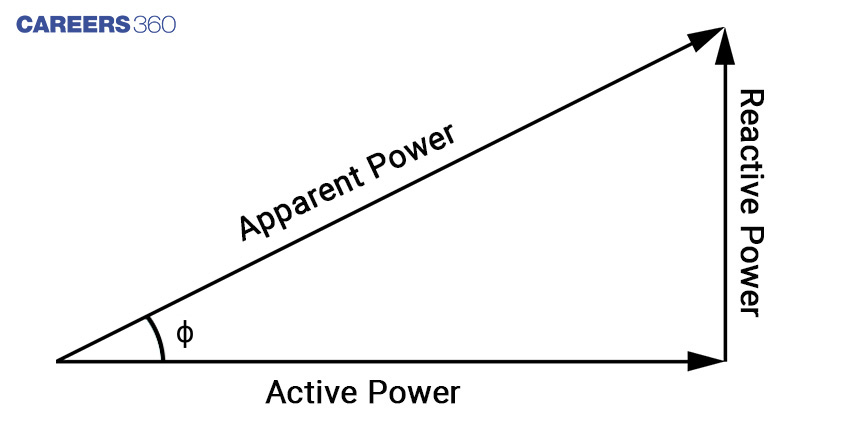
1653630747576

From the power triangle ɸ can be computed using different trigonometric ratios.

cosɸ=Active Power/Apparent Power

sinɸ=Reactive Power/Apparent Power

tanɸ=Reactive Power/ Active Power

Some Points To Remember

For a purely resistive circuit the instantaneous current is in phase with the instantaneous voltage. That is for V_S=V_msinωt, the current I=I_msinωt.
For a purely inductive circuit, the instantaneous voltage leads the current by 900. That is if V_S=V_msinωt, I=I_msin(ωt-?/2)
For a purely capacitive circuit, the instantaneous voltage lags the current by 900. That is if V_S=V_msinωt, I_S=I_msin(ωt+?/2)
For a series RLC circuit if source voltage V_S=Vmsinωt, IS=I_msin(ωt-ɸ) and the value of ɸ may be positive or negative depending on the value of inductive and capacitive reactance. If X_L>X_C, the current lags behind the voltage. If X_C>X_L current leads to the voltage.

NEET 2026 Free Mock Test with Solutions

Download the NEET 2026 Free Mock Test PDF with detailed solutions. Practice real exam-style questions, analyze your performance, and enhance your preparation.

Download EBook

Question: (JEE Main 2019)

An alternating voltage V(t)=220sin100?t volt is applied to a purely resistive load of 50Ω. The time taken for the current to rise from half of the peak value to the peak value is:

Solution-

I₀/2=I₀sinωt

I₀/2I₀=sinωt

½=sinωt

ωt=?/6

Given ω=100?

100?t=?/6, therefore t=1/600 or =1..67milli seconds. This is the time to reach half the peak value from zero.

Peak value occurs at ωt=?/2. So time taken to reach peak value from zero=1/200=5milli seconds.

The time taken from half of the peak to the peak value=5-1.67=3.3milli seconds

Series Resonance

Resonance is the characteristic of the RLC series circuit. Resonance occurs when the value of capacitive and inductive reactance are equal(X_C=X_L). The frequency at which X_C=X_L is known as resonant frequency ⍵₀. At ⍵₀, X_C-X_L=0, impedance becomes minimum and current I become maximum and I_max=V_max/R. And the value of resonant frequency is-

$w_0=\frac{1}{\sqrt{LC}}$

And the power factor at resonance=1

Frequency Response Or Resonant Curve

The curve represents the variation of current amplitude with respect to frequency.

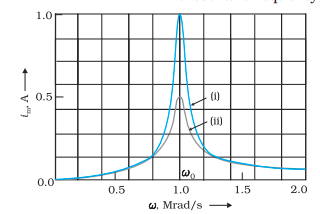
1653630746608

The sharpness of resonance is measured by the quality factor Q.

Q=⍵₀L/R. Also

Q=1/(⍵₀RC)

As Q increases the sharpness also increases. From the frequency response, we can say that the Q factor of (i) is greater than the Q factor of (ii) as the sharpness of the first curve is more.

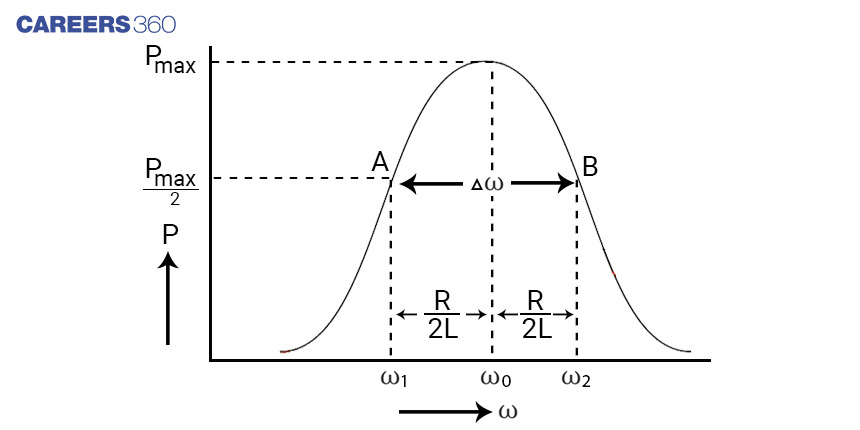
Suppose we choose a frequency other than ⍵0 such that the current magnitude is 1/√2 times the maximum value or power dissipated by the circuit is half of maximum value. There will be two such frequencies for which the current magnitude is 1/√2 times the maximum value, ⍵₁<⍵₀ and ⍵₂>⍵₀. The magnitude of ⍵₀-⍵₁=⍵₂-⍵₀ =?⍵. Here ⍵1 and ⍵2 are half power frequencies.

The difference ⍵₂-⍵₁ = 2?⍵ is known as the bandwidth and bandwidth 2?⍵= R/L. Therefore Q=⍵₀L/R =⍵₀/2?⍵=⍵₀/(⍵₂-⍵₁)

1653630752934

Past 6 Years NEET Questions On RLC Series Circuit

NEET 2016

An inductor 20 mH, a capacitor 50 ?F and a resistor 40 Ω are connected in series across a source of emf V = 10 sin 340 t. The power loss in the A.C circuit-

Solution

Power loss in the circuit is asked. We have to find the average power.

Given V_m=10, ⍵=340. To find the average power we need to find Im and cosɸ

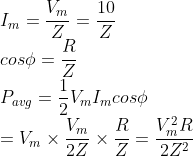
$\\I_m=\frac{V_m}{Z}=\frac{10}{Z} \\cos\phi=\frac{R}{Z}\\P_{avg}=\frac{1}{2}V_mI_mcos\phi\\=V_m\times\frac{V_m}{2Z}\times\frac{R}{Z}=\frac{V_m^2R}{2Z^2}\\\\$

$Z=\sqrt{R^2+(\omega L-\frac{1}{\omega})^2}$

$=\frac{1}{2}\left [ \frac{100\times40}{1600+(340\times20\times10^{-3}-\frac{1}{340\times50\times10^{-6}})^2} \right ]\\=\frac{2000}{1600+(6.8-58.82)^2}\\=\frac{2000}{4306}=0.464W$

NEET 2018

An inductor 20 mH, a capacitor 100 ?F and a resistor 50 Ω are connected in series across a source of emf V = 10 sin 314 t. The power loss in the circuit is

Solution: 0.79W

This question is similar to the NEET 2016 question and the values only differ. Try to solve it yourself.

NEET 2021

An inductor of inductance L, a capacitor of capacitance C and a resistor of resistance 'R' are connected in series to an ac source of potential difference 'V' volts as shown in the figure.

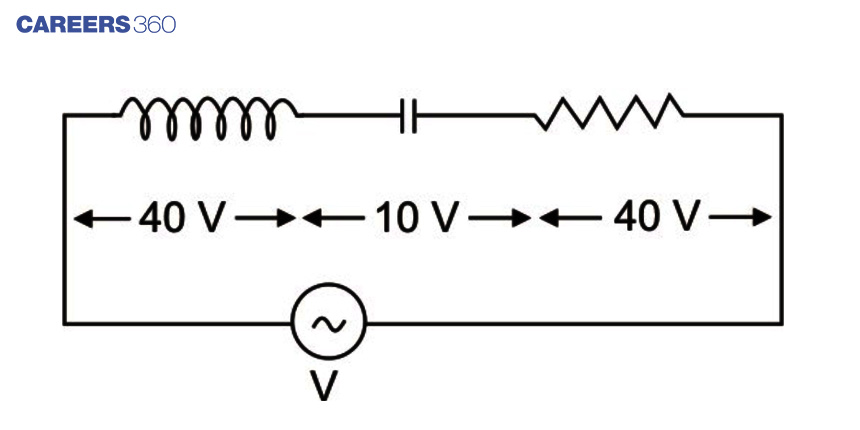
1653630751867

The potential difference across L, C and R is 40 V, 10V and 40V, respectively. The amplitude of the current flowing through the LCR series circuit is 10√2 A. The impedance of the circuit is-

Solution:

Z=V_rms / I_rms

$\\Z=\frac{\sqrt{V_R^2+(V_L-V_C)^2}}{I_{rms}}\\=\frac{\sqrt{40^2+30^2}}{10\sqrt{2}/\sqrt{2}}=5\Omega$

NEET 2020

A series of LCR circuits is connected to an ac voltage source. When L is removed from the circuit, the phase difference between current and voltage is ?/3 If instead C is removed from the circuit, the phase difference is again ?/3 between current and voltage. The power factor of the circuit is

Solution:

$\begin{aligned} &\text { For only } \mathrm{RC}:\phi_{\mathrm{RC}}=\frac{\pi}{3}\\ &\tan \left(\frac{\pi}{3}\right)=\frac{\mathrm{X}_{\mathrm{c}}}{\mathrm{R}} \Rightarrow \mathrm{X}_{\mathrm{c}}=\sqrt{3} \mathrm{R}\\ &\text { For only } \mathrm{RL}:\phi_{\mathrm{RL}}=\frac{\pi}{3}\\ &\tan \left(\frac{\pi}{3}\right)=\frac{\mathrm{X}_{\mathrm{L}}}{\mathrm{R}} \Rightarrow \mathrm{X}_{\mathrm{L}}=\sqrt{3} \mathrm{R}\\ &\text { For RLC:- }\\ &\tan (\phi)=\frac{\mathrm{X}_{\mathrm{L}}-\mathrm{X}_{\mathrm{C}}}{\mathrm{R}}=\frac{\sqrt{3} \mathrm{R}-\sqrt{3} \mathrm{R}}{\mathrm{R}}=0 \Rightarrow \phi=0 \Rightarrow \cos \phi=1 \end{aligned}$

NEET 2021

A series LCR circuit containing 5.0 H inductor 80 capacitor ?F and 40Ω resistor is connected to a 230 V variable frequency ac source. The angular frequencies of the source at which power transferred to the circuit is half the power at the resonant angular frequency are likely to be:

(1) 25 rad/s and 75 rad/s (2) 50 rad/s and 25 rad/s (3) 46 rad/s and 54 rad/s (4) 42 rad/s and 58 rad/s

Solution:

Power =P_o/2 for half power frequencies. 2?⍵ the Bandwidth of resonance curve= R/L

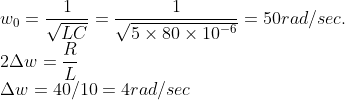
$\\w_0=\frac{1}{\sqrt{LC}}=\frac{1}{\sqrt{5\times80\times 10^{-6}}}=50rad/sec.\\2\Delta w=\frac{R}{L}\\\Delta w=40/10=4rad/sec$

$\\w_0-w_1=4\\w_1=50-4=46rad/s$

$\\w_2-w_0=4\\w_2=50+4=54rad/s$

So at 46 rad/s and 54 rad/s P=P₀/2

So option (3) 46 rad/s and 54 rad/s is right

Practice Question

A series LCR circuit driven by 300 V at a frequency of 50 Hz contains a resistance $R= 3k\Omega$ , an inductor of inductive reactance $X_{L}= 250\pi\, \Omega$ and an unknown capacitor. Find the value of capacitance to maximize the average power
In a series LCR circuit, the inductive reactance (XL) is 10 $\Omega$ and the capacitive reactance (XC) is 4 $\Omega$ . The resistance (R) in the circuit is 6 $\Omega$ . What is the power factor of the circuit?
An AC circuit has $R=100 \Omega, C= 2\mu F$ and L = 800 mH, connected in series. Find the quality factor of the circuit.

Articles

Kerala NEET Merit List 2026: Download Kerala MBBS Merit List PDF

1 day ago

Counselling

Kerala NEET Counselling 2026: Dates, Registration, Allotment Result

1 day ago

Counselling

IPU NEET Counselling 2026: Round 1 Schedule, Registration, Process, Result

1 day ago

Counselling

HP NEET Merit List 2026 - Release Date and PDF Download Link

1 day ago

Counselling

Upcoming Medicine Exams

Haryana BSc Nursing

Ongoing Dates

Haryana BSc Nursing Counselling Date

17 Jan'26 - 19 Jan'26 (Online)

Karnataka Common Entrance Test for BSc Nursing

Ongoing Dates

KCET BSc Nursing Application Date

17 Jan'26 - 17 Feb'26 (Online)

Result

Exam Pattern

Admit Card

Maharashtra Bachelor of Science in Nursing Common Entrance Test

Upcoming Dates

MH BSc Nursing CET Exam Date

6 May'26 - 7 May'26 (Online)

Admit Card

Exam Pattern

Result

Certifications By Top Providers

Biomolecules Structure Function in Health and Disease

Via All India Institute of Medical Sciences New Delhi

Industrial Biotechnology

Via Indian Institute of Technology Kharagpur

Certificate Course in Biostatistics, Epidemiology and Research Methodology

Via Manipal Academy of Higher Education, Manipal

Nutrition in the Health Sector

Via The University of Adelaide, Adelaide

Pathology

Via Tsinghua University, Beijing

Online M.Sc Psychology

Via Centre for Distance and Online Education, Andhra University

355 courses

310 courses

233 courses

191 courses

106 courses

Johns Hopkins University, Baltimore

75 courses

Biology and Life Sciences

Health, Fitness and Medicine

Psychology

Health Care Management

Explore Top Universities Across Globe

University College London, London

Gower Street, London, WC1E 6BT

University of Essex, Colchester

Wivenhoe Park Colchester CO4 3SQ

University of Nottingham, Nottingham

University Park, Nottingham NG7 2RD

University of Wisconsin, Madison

329 Union South 1308 W. Dayton Street Madison, WI 53715-1149

University of Alberta, Edmonton

116 St. and 85 Ave., Edmonton, Alberta, Canada T6G 2R3

Keele University, Newcastle

Staffordshire, UK, ST5 5BG

General Medicine and Surgery

Bio-Chemistry

Top Engineering Colleges in Germany - Check List, How to apply, Fees

11 min ⋆ Nov 28, 2025 07:11 AM IST

MBA in Italy for Indian Students 2026: Fees, Colleges, Requirements

6 min ⋆ Nov 28, 2025 04:11 AM IST

Proof of Funds List for Germany Student Visa in 2026

5 min ⋆ Nov 28, 2025 04:11 AM IST

Universities in Canada with No Application Fee for International Students 2026

5 min ⋆ Nov 28, 2025 04:11 AM IST

Intakes in Canada 2026 (Fall, Winter & Summer): How to Apply

5 min ⋆ Nov 27, 2025 04:11 AM IST

Study MBBS in Russia 2026: MBBS Fees, Colleges & Requirements

19 min ⋆ Nov 27, 2025 04:11 AM IST

Popular Courses and Specializations

Popular Degrees

Popular Branches

List of colleges accepting NEET

All India Institute of Medical Sciences New Delhi

Courses & FeesCut-offsAdmissionsPlacementsReviews

All India Institute of Medical Sciences Rishikesh

Courses & FeesCut-offsAdmissionsPlacementsReviews

Christian Medical College, Vellore

Courses & FeesCut-offsAdmissionsPlacementsFacilities

Atal Bihari Vajpayee Institute of Medical Sciences and Dr Ram Manohar Lohia Hospital, New Delhi

Courses & FeesCut-offsAdmissionsPlacementsFacilities

Ayurved Mahavidyalaya and Seth R V Ayurved Hospital, Mumbai

Courses & FeesCut-offsAdmissionsFacilitiesQues. & Ans

Ashtang Ayurved Mahavidyalaya, Pune

Courses & FeesCut-offsAdmissionsFacilitiesQues. & Ans

Browse Medicine Colleges by State

Maharashtra

Uttar Pradesh

Karnataka

Tamil Nadu

Kerala

Telangana

Questions related to NEET

On Question asked by student community

Have a question related to NEET ?

Excluding NEET/MBBS, what career options for PCB students currently have high demand, job availability, and long-term stability in India?

Hello,

Here are good career options for PCB students in India (excluding NEET/MBBS) that have high demand, jobs available, and long-term stability :

1. Biotechnology

Study: B.Sc/ B.Tech/ M.Sc in Biotechnology.
Jobs: Research, labs, pharma, agriculture biotech.
Why: Growing field with many industries.

2. Pharmacy

Study: B.Pharm, M.Pharm.
Jobs: Pharmacist,

Read Complete Answer

Prachi Kumari

11 Jan'26

Is the NEST exam much harder than NEET?

HELLO,

Yes , the NEST exam is generally considered tougher than NEET as it requires more focus towards conceptual understanding and thinking , while NEET generally tests NCERT based knowledge where as in NEST it requires you to have deeper clarity in Physics , Chemistry , Biology and Mathematics.

NEET

Read Complete Answer

Devanshi Goyal

10 Jan'26

Neet bio 2026 digram pyq preparation

Hello,

The National Eligibility cum Entrance Test (NEET) is conducted by the National Testing Agency (NTA) for admission to medical and dental colleges in India. Biology is the most important section in NEET as it carries 360 marks, which is half of the total score, with 45 questions each from

Read Complete Answer

Pawni Goyal

8 Jan'26

Previous 3 years question paper neet

HELLO,

Below i am attaching the link through which you can easily access the previous three year question paper of NEET with solutions PDF

Here is the link :- https://medicine.careers360.com/download/sample-papers/neet-previous-year-question-papers-solutions-pdf

Hope this will help you!

Read Complete Answer

Devanshi Goyal

10 Jan'26

What other options do pcb students have besides neet and cuet

Hi there,

Apart from NEET and CUET you can explore the following career paths to

Students pursuing the PCB (Physics, Chemistry, Biology) stream can explore a wide range of options apart from CUET and NEET. Their choices are not just limited to medicine and can expand to include numerous areas

Popular NEET Questions

Column I ( Salivary gland)		Column II ( Their location)
Parotids	I	Below tongue
Sub-maxillary / sub-mandibular	Ii	Lower jaw
Sub-linguals	Iii	Cheek

Option: 1

a(i), b(ii) , c(iii)

Option: 2

a(ii), b(i), c(iii)

Option: 3

a(i), b(iii), c(ii)

Option: 4

a(iii), b(ii), c(i)

Read Complete Answer

$Ethyl \; ester \xrightarrow[(excess)]{CH_{3}MgBr} P$

the product 'P' will be ,

Option: 1

Option: 2

Option: 3

$\left ( C_{2}H_{5} \right )_{3} - C- OH$

Option: 4

Read Complete Answer

	Valve name		Function
I	Aortic valve	A	Prevents blood from going backward from the pulmonary artery to the right ventricle.
II	Mitral valve	B	Prevent blood from flowing backward from the right ventricle to the right atrium.
III	Pulmonic valve	C	Prevents backward flow from the aorta into the left ventricle.
IV	Tricuspid valve	D	Prevent backward flow from the left ventricle to the left atrium.

Option: 1

I – A , II – B, III – C, IV – D

Option: 2

I – B , II – C , III – A , IV – D

Option: 3

I – C , II – D , III – A , IV – B

Option: 4

I – D , II – A , III – B , IV – C

Read Complete Answer

Column A	Column B
A	a) Organisation of cellular contents and further cell growth.
B	b) Leads to formation of two daughter cells.
C	c) Cell grows physically and increase volume proteins,organells.
D	d) synthesis and replication of DNA.

Match the correct option as per the process shown in the diagram.

Option: 1

1-b,2-a,3-d,4-c

Option: 2

1-c,2-b,3-a,4-d

Option: 3

1-a,2-d,3-c,4-b

Option: 4

1-c,2-d,3-a,4-b

Read Complete Answer

0.014 Kg of N₂ gas at 27 ⁰C is kept in a closed vessel. How much heat is required to double the rms speed of the N₂ molecules?

Option: 1

3000 cal

Option: 2

2250 cal

Option: 3

2500 cal

Option: 4

3500 cal

Read Complete Answer

0.16 g of dibasic acid required 25 ml of decinormal $NaOH$ solution for complete neutralisation. The modecular weight of the acid will be

Option: 1

Option: 2

Option: 3

128

Option: 4

256

Read Complete Answer

0.5 F of electricity is passed through 500 mL of copper sulphate solution. The amount of copper (in g) which can be deposited will be:

Option: 1

31.75

Option: 2

15.8

Option: 3

47.4

Option: 4

63.5

Read Complete Answer

0.5 g of an organic substance was kjeldahlised and the ammonia released was neutralised by 100 ml 0.1 M HCl. Percentage of nitrogen in the compound is

Option: 1

Option: 2

Option: 3

Option: 4

Read Complete Answer

0xone is

Option: 1

$\mathrm{KO}_{2}$

Option: 2

$\mathrm{Na}_{2} \mathrm{O}_{2}$

Option: 3

$\mathrm{Li}_{2} \mathrm{O}$

Option: 4

$\mathrm{CaO}$

Read Complete Answer

(1) A substance known as "Smack"

(2) Diacetylmorphine

(3) Possessing a white color

(4) Devoid of any odor

(5) Crystal compound with a bitter taste

(6) Obtained by extracting from the latex of the poppy plant

The above statements/information are correct for:

Option: 1

Morphine

Option: 2

Heroin

Option: 3

Cocaine

Option: 4

Barbiturates

Read Complete Answer

Begin a career in Medical and Allied Sciences. Admissions Open for

JSS University Mysore 2025

Apply

NAAC A+ Accredited| Ranked #24 in University Category by NIRF | Applications open for multiple UG & PG Programs

Virohan Allied & Healthcare Programs

Apply

Allied & Healthcare programs | 20+ Partner Universities & Institutes | 98% placement record

Amity University-Noida Health and Allied Sciences Admissions

Apply

Amongst top 3% universities globally (QS Rankings) | Wide Range of scholarships available

View all Application Forms

NEET Notifications

NEET aspirant death: Prashant Kishor questions police probe, seeks re-investigation

Press Trust of India

Jan 16, 2026

JK NEET PG 2025: Round 3 registrations reopens for MD, MS; apply by January 20

Sundararajan

Jan 16, 2026

KNRUHS revises Telangana NEET PG 2025 merit list; 1,891 eligible for management quota seats

Vaishnavi Shukla

Jan 15, 2026

Gujarat NEET PG Counselling 2025: MCC reopens round 3 registration at medadmgujarat.org

Sundararajan

Jan 15, 2026

NEET UG 2026 LIVE: NTA NEET syllabus out at neet.nta.nic.in; NEET brochure expected soon, updates

Durva Gupta

Jan 12, 2026

NCAHP notifies UGC: NEET UG must for physiotherapy, university tests for psychology courses

Musab Qazi

Jan 10, 2026

Punjab NEET PG round 3 registration deadline extended to January 8 for MD, MS

Sundararajan

Jan 07, 2026

Latest updates

NEET Important Biology Diagrams 2026: Biology Diagrams Class 11th & 12th

Jan 17, 2026

Kerala NEET Merit List 2026: Download Kerala MBBS Merit List PDF

Jan 17, 2026

Kerala NEET Counselling 2026: Dates, Registration, Allotment Result

Jan 17, 2026

IPU NEET Counselling 2026: Round 1 Schedule, Registration, Process, Result

Jan 17, 2026

IPU NEET Application Form 2026, Registration: Release Date, Process, Fees

Jan 17, 2026

View all

Explore Career Options

By Industry

Orthotist and Prosthetist

Orthotists and Prosthetists are professionals who provide aid to patients with disabilities. They fix them to artificial limbs (prosthetics) and help them to regain stability. There are times when people lose their limbs in an accident. In some other occasions, they are born without a limb or orthopaedic impairment. Orthotists and prosthetists play a crucial role in their lives with fixing them to assistive devices and provide mobility.

6 Jobs Available

Pathologist

A pathologist is required to examine body fluids, tissues, and organs with the help of laboratory tests and microscopic examinations. Pathologists often work in hospitals and diagnostic labs, often assisting doctors when it comes to treatment decisions. Due to the increased demand for diagnostic services, pathology offers good career opportunities in clinical practices, research and academics.

5 Jobs Available

Veterinary Doctor

A Veterinarian is responsible for diagnosing, treating, and preventing diseases in animals. The individual performs surgeries, guides nutrition, and provides animal care. A Bachelor’s in Veterinary Science (B.Vsc.) is a mandatory degree. The profession brings together medical knowledge and a strong commitment to animal welfare.

5 Jobs Available

Speech Therapist

A Speech Therapist (Speech-Language Pathologist) diagnoses and treats speech, language, communication, and swallowing disorders across all ages. They work in hospitals, schools, clinics, and more. Becoming an SLP requires a master’s degree, clinical training, and certification. With rising demand, the career offers rewarding opportunities in therapy, education, and research.

4 Jobs Available

Gynaecologist

A gynaecologist is a medical specialist in women’s reproductive health, handling issues like menstruation, fertility, pregnancy, and childbirth. They perform exams, surgeries, and offer family planning services. To become one, students must complete MBBS and postgraduate training. Gynaecologists work in hospitals or clinics and are in high demand, with salaries growing significantly with experience.

4 Jobs Available

Audiologist

The audiologist career involves audiology professionals who are responsible to treat hearing loss and proactively preventing the relevant damage. Individuals who opt for a career as an audiologist use various testing strategies with the aim to determine if someone has a normal sensitivity to sounds or not. After the identification of hearing loss, a hearing doctor is required to determine which sections of the hearing are affected, to what extent they are affected, and where the wound causing the hearing loss is found. As soon as the hearing loss is identified, the patients are provided with recommendations for interventions and rehabilitation such as hearing aids, cochlear implants, and appropriate medical referrals. While audiology is a branch of science that studies and researches hearing, balance, and related disorders.

3 Jobs Available

Oncologist

An oncologist is a medical doctor who diagnoses and treats cancer using chemotherapy, radiation, surgery, and other therapies. They work with a team to create treatment plans tailored to each patient. Specialisations include medical, surgical, radiation, pediatric, gynecologic, and hematologic oncology. Becoming an oncologist in India requires an MBBS and postgraduate studies in oncology.

3 Jobs Available

Biochemist

A biochemist studies the chemical processes within living organisms, combining chemistry and biology. They conduct experiments, analyse data, and develop products like drugs and vaccines. Biochemists work in labs, healthcare, research, and education. A degree in biochemistry or related fields is essential, with advanced roles often requiring higher degrees. They also ensure quality control and may teach or mentor others.

2 Jobs Available

Never miss NEET update

Get timely NEET updates directly to your inbox. Stay informed!

Student Community: Where Questions Find Answers

Ask and get expert answers on exams, counselling, admissions, careers, and study options.

Download Careers360 App

All this at the convenience of your phone

Regular Exam Updates
Best College Recommendations
College & Rank predictors
Detailed Books and Sample Papers
Question and Answers

Scan and download the app

Applications Open

NEET Mock Test

NEET Previous Year Papers’ Analysis: LCR Circuits, Concepts And Solutions

LCR Series Circuit

Force Voltage Analogy

JSS University Mysore 2025

Virohan Allied & Healthcare Programs

NEET

NEET AYUSH All India Counseling

Maharashtra MBBS/BDS Counselling

Arunachal Pradesh MBBS/BDS Admissions

NEET AYUSH All India Counseling

VMMC - Safdarjung Hospital - Vardhman Mahavir Medical College and Safdarjung Hospital, New Delhi

Atal Bihari Vajpayee Institute of Medical Sciences and Dr Ram Manohar Lohia Hospital, New Delhi

Maharashtra MBBS/BDS Counselling

GSMC Mumbai - Seth GS Medical College, Mumbai

LTMMC Mumbai - Lokmanya Tilak Municipal Medical College, Sion, Mumbai

Arunachal Pradesh MBBS/BDS Admissions

KGMU Lucknow - King George's Medical University, Lucknow

Dr R Ahmed Dental College and Hospital, Kolkata

NEET UG

AIIMS Delhi - All India Institute of Medical Sciences New Delhi

VMMC - Safdarjung Hospital - Vardhman Mahavir Medical College and Safdarjung Hospital, New Delhi

Karnataka MBBS/BDS Counselling

BMCRI Bangalore - Bangalore Medical College and Research Institute, Bangalore

ESI Post Graduate Institute of Medical Sciences and Research, Bangalore

UP MBBS/BDS Counselling

KGMU Lucknow - King George's Medical University, Lucknow

Dr Ram Manohar Lohia Institute of Medical Sciences, Lucknow

Gujarat MBBS/BDS Counselling

BJMC Ahmedabad - B J Medical College, Ahmedabad

GMERS Medical College and Hospital, Sola

Madhya Pradesh MBBS/BDS Counselling

Gandhi Medical College, Bhopal

Gajra Raja Medical College, Gwalior

Kerala MBBS/BDS Counselling

Government Medical College, Kozhikode

Government Medical College, Thiruvananthapuram

Tamil Nadu MBBS/BDS Counselling

MMC Chennai - Madras Medical College, Chennai

Stanley Medical College, Chennai

Telangana MBBS/BDS Counselling

Osmania Medical College, Hyderabad

ESIC Medical College, Hyderabad