Isobaric Process MCQ - Practice Questions with Answers

Isobaric Process- A Thermodynamic process in which pressure remains constant is known as the isobaric process.

In this process, V and T change keeping P constant. I.e Charle’s law is obeyed in this process

   Key points in the Isobaric Process-

• Its Equation of state is given as $\frac{V}{T}=$ constant

$$
\text { І.e } \frac{V_1}{T_1}=\frac{V_2}{T_2}=\text { constant }
$$

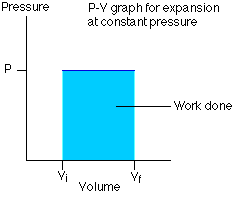
• - P-V Indicator diagram for an isobaric process. Its PV graph has slope $=0$ (i.e $\frac{d P}{d V}=0$,

The above Graph represents an isobaric expansion.

 The P-V diagram for this process is a line parallel to the volume line.

- Specific heat of gas during the isobaric process is given by

$$
C_P=\left(\frac{f}{2}+1\right) R
$$

- The bulk modulus of elasticity during the isobaric process is given by

$$
K=\frac{\Delta P}{-\Delta V / V}=0
$$

- Work done in the isobaric process-

$$
\Delta W=\int_{V_i}^{V_f} P d V=P \int_{V_i}^{V_f} d V=P\left[V_f-V_i\right]
$$

Or we can write $\Delta W=P\left(V_f-V_f\right)=n R\left[T_f-T_t\right]=n R \Delta T$
- Internal energy in an isobaric process

$$
\Delta U=n C_V \Delta T=n \frac{R}{(\gamma-1)} \Delta T
$$
 

- Heat in an isobaric process

From FLTD $\Delta Q=\Delta U+\Delta W$

$$
\begin{aligned}
& \qquad \begin{aligned}
\Delta Q & =n \frac{R}{(\gamma-1)} \Delta T+n R \Delta T=n R \Delta T\left[\frac{1}{\gamma-1}+1\right] \\
\Rightarrow \Delta Q & =n R \Delta T \frac{\gamma}{\gamma-1}=n\left(\frac{\gamma}{\gamma-1}\right) R \Delta T=n C_p \Delta T
\end{aligned} \\
& \text { So } \Delta Q=n C_p \Delta T
\end{aligned}
$$

- Examples of the isobaric process-
1. Conversion of water into vapor phase (boiling process)

From the first law of thermodynamics

$$
\Delta Q=\Delta U+\Delta W=\Delta U_K+\Delta U_P+\Delta W
$$

since $\Delta U_K=0$ [as there is no change in temperature] and using, $\Delta Q=m L$

$$
\begin{aligned}
\Delta Q & =\Delta U_P+P\left[V_f-V_t\right] \\
\Delta U_P & =\Delta Q-P\left[V_f-V_t\right] \\
\Delta U_P & =m L-P\left[V_f-V_i\right]
\end{aligned}
$$

2. Conversion of ice into water

From FLOT $\Delta Q=\Delta U+\Delta W$ and using, $\Delta Q=m L$
we get $m L=\Delta U_P+\Delta U_K+\Delta W$

$$
m L=\Delta U_P+\Delta U_K+P\left(V_f-V_i\right)
$$

since $\Delta U_K=0$ [as there is no change in temperature]
and $\Delta W=0$ [As $V_f-V_{i \text { is negligible, I.e, when ice converts into water then changes }}$ in volume, is negligible]
Hence $\Delta U_P=m L$