Magnetic Field Due To Circular Current Loop - Practice Questions & MCQ

Magnetic Field due to circular current loop at its centre: 

Magnetic Field due to circular coil at Centre-

where N=number of turns, i= current and r=radius of a circular coil.

Similarly, if  Arc subtends angle theta at the centre as shown below then 

 

similarly, if Arc subtends angle () at the centre then

So the magnetic field of Semicircular arc at the centre is 

So Magnetic field due to three quarter Semicircular Current-Carrying arc at the centre is 

• The direction of the magnetic field-

Right-Hand Thumb Rule gives the direction of the magnetic field of Circular Currents.

Right-hand thumb rule stated below:

If the fingers are curled along the current, the stretched thumb will point towards the magnetic field.

1. If the current is in a clockwise direction then the direction of the magnetic field is away from the observer or perpendicular inwards.

2. If the current is in anti-clockwise direction then the direction of the magnetic field is towards the observer or perpendicular outwards

• Special cases-

1. If the  Distribution of current across the diameter-

  then 

2. if Current between any two points on the circumference-

Then 

 

3.Concentric co-planar circular loops carrying the same current in the Same Direction-

 

  

If the direction of currents are the same in concentric circles but having a different number of turns then 

 

 

4.Concentric co-planar circular loops carrying the same current in the opposite Direction-

 

 

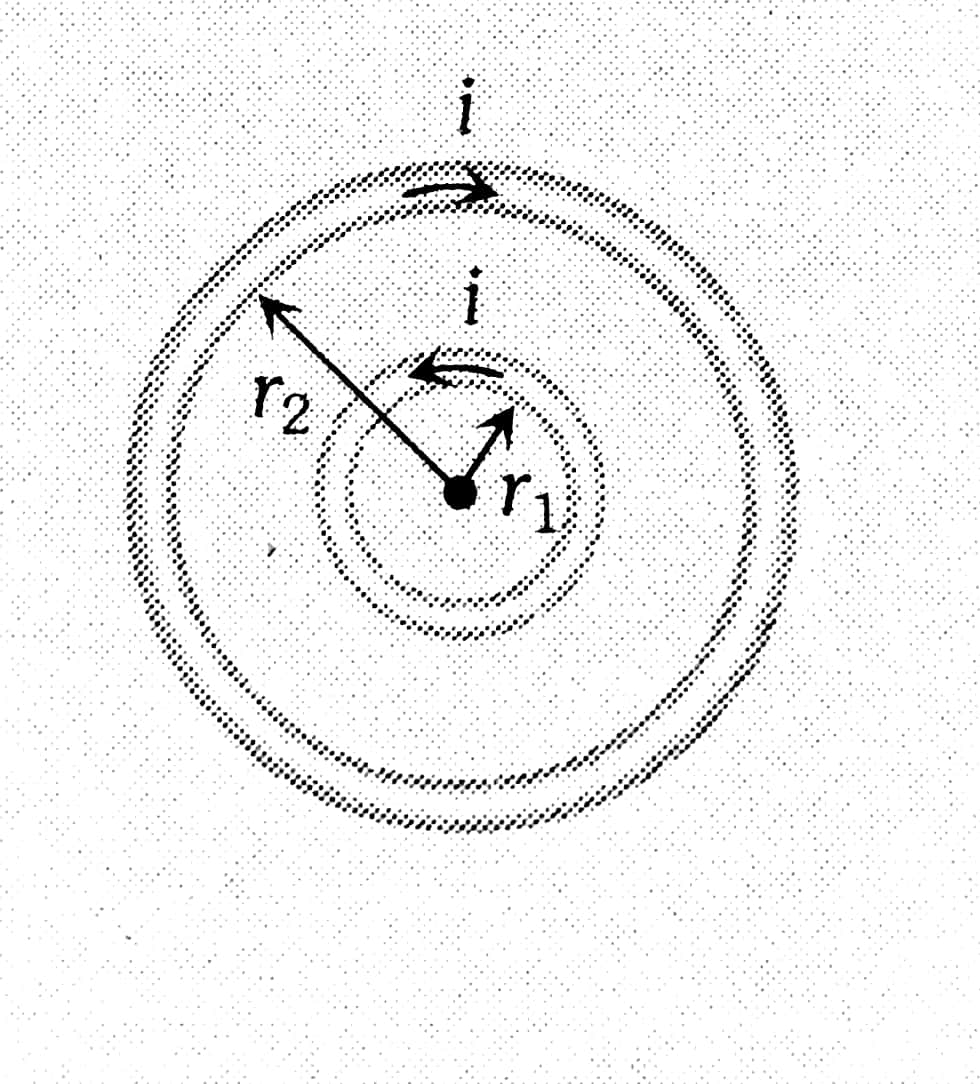
If the number of turns is not the same i.e 

5.  Concentric loops but their planes are perpendicular to each other-

Then 

 

6. Concentric loops but their planes are at an angle ϴ with each other-