Apply to Amrita Vishwa Vidyapeetham Allied & Life Science 2024
Refraction And Dispersion Of Light Through A Prism - Practice Questions & MCQ
Quick Facts
-
Refraction Through A Prism 1, Refraction Through A Prism 2, Dispersion Of Light 1 is considered one of the most asked concept.
-
51 Questions around this concept.
Solve by difficulty
The angle of incidence for a ray of light at a refracting surface of a prism is 45°. The angle of the prism is 60°. If the ray suffers minimum deviation through the prism, the angle of minimum deviation and refractive index of the material of the prism respectively, are:
The refracting angle of a prism is A, and refractive index of the material of the prism is cot(A/2). The angle of minimum deviation is:
A ray of light is incident at an angle of incidence i, on one face of prism of angle A (assumed to be small) and emerges normally from the opposite face. If the refractive index of the prism is , the angle of incidence i is nearly equal to:
The angle of a prism is 'A'. One of its reflecting surfaces is silvered. Light rays falling at an angle of incidence 2A on the first surface returns back through the same path after suffering reflection at the silvered surface. The refractive index , of the prism is:
A beam of light consisting of red, green and blue colours is incident on a right angled prism. The refractive index of the material of the prism for the above red, green and blue wavelengths are 1.39, 1.44 and 1.47, respectively.

The prism will:
A glass prism of refractive index 1.5 is immersed in water . A light beam incident normally on the face A B is totally reflected to reach the face B C if

A luminous object is placed at a distance of 30cm from the convex lens of focal length 20cm. On the other side of the lens, at what distance from the lens, a convex mirror of radius of curvature 10cm be placed in order to have an upright image of the object coinciding with it
In the figure shown a convex mirror of radius of curvature 20 cm is shown. An object O is placed in front of this mirror. Its ray diagram is shown. How many mistakes are there in the ray diagram (AB is its principal axis):

A ray of light is incident on the face of the equilateral triangle at an incident angle of 50o. At this angle, minimum deviation occurs. This deviation is
An equilateral prism has an angle of deviation when the angle of incidence is
. The angle of deviation if a ray is incident normally on a surface is:
Concepts Covered - 4
A prism is a transparent medium whose refracting surfaces are not parallel but are inclined to each other at an angle A which is also known as angle of the prism.

The angle of deviation -It is the angle between the emergent and the incident ray.
For the above figure
and using
Note-From the above formula, we can say that if we interchange i and e then also we will get the same value of .
- The plot of

As shown in the above figure The graph is a parabola.
If we vary i between
then the value of
decreases
and the value of
increases
And when
and when
- Grazing Incidence-When i = 90°, the incident ray grazes along the surface of the prism. This is known as grazing incidence.
- Grazing Emergence- When e = 90°, the emergent ray grazes along the prism surface. This is known as grazing emergence.
This happens when the light ray strikes the second face of the prism at the critical angle for glass - air.
I.e For the prism of refractive index places in the air.
then then e = 90°
Refractive index of prism in case of minimum deviation condition-
As we learned The angle of deviation for the prism is given as
and from The plot of we get

For the prism of refractive index places in the air.
For the first surface, we can write
similarly For the second surface, we can write
using i=e we get
So will give us
- For thin films (i.e
)
Then
and
So we get
- condition of no emergence-
i.e A ray of light incidence on a prism of angle A & Refractive index will not emerge out of a prism
This will happen when
where critical angle
Dispersion of light -The splitting of white light into its constituent colors or wavelengths is called dispersion of light.
or
angular splitting of a ray of white light into a number of components and spreading in different directions is called diversion of light.
This phenomenon arises due to the fact that the refractive index varies with wavelength.
When white light is incident on the prism it will split itself into its constituent colors as shown in the below figure.
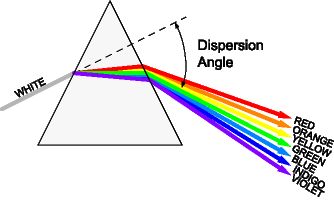
The deviation is given as
- Angular dispersion (
)- Angular separation between extreme colors
i.e
It depends upon and A.
- Dispersive power (ω)- Ratio of angular dispersion to mean deviation.
i.e
where where is deviation of mean ray (especially yellow)
where
= Refractive index of violet
Refractive index of red
Refractive index of yellow
Condition for deviation without dispersion-
This means an achromatic combination of two prisms in which net(or) resultant dispersion is 0, but and deviation is produced as shown in the below figure.
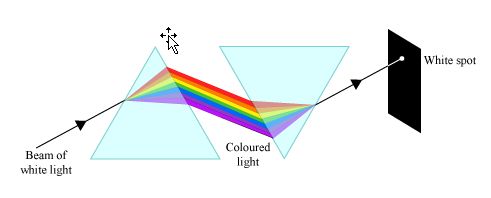
where
= Refractive index of violet ( prism 1)
Refractive index of red ( prism 1)
= Refractive index of violet ( prism 2)
Refractive index of red ( prism 2)
Similarly
where are the dispersive powers of the two prisms and their corresponding mean deviations are
.
Condition for Dispersion without deviation-
A combination of two prisms in which deviation produced for the mean ray by the first prism is equal and opposite to that produced
by the second prism will give a dispersion of light without deviation.
This combination of two prisms is also called a direct vision prism.
i.e

As shown in the above figure as emergent rays from the second prism is parallel to the incident white ray of the prism 1.
this will give .
and the Angular dispersion is given as
Study it with Videos
"Stay in the loop. Receive exam news, study resources, and expert advice!"











