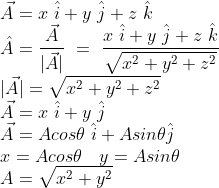Vector algebra is one of the fundamental topics of algebra. There are two types of physical quantities – scalar quantity and vector quantity. In vector algebra, we study the vector quantities. Vector quantity is a quantity that has both magnitude and direction and follows vector addition rules whereas scalar quantity only has magnitude.

This Story also Contains

Vectors Addition Rules
Subtraction And Addition Of Vectors
Multiplication Of Vectors
Other Important Formulas
Logarithmic
Exponential
Exponential Function Rules
NEET Previous Five Years’ Analysis
Previous Years Questions To Understand The Concepts

NEET Five-Year Analysis: Solving Vectors Algebra, Logarithmic, And Exponential Questions

NEET Vector Algebra(Image: Shutterstock)

Vector: A vector is a measurement or quantity that includes both magnitude and direction. Generally, it can be represented physically by an arrow, and mathematically as A⃗ can be read as “A vector”. Arrow (➙) indicates the direction of the vector and its length represents the magnitude of the vector that is given in the following figure. |A⃗| represents the magnitude of the vector A. If we say that two vectors are equal, then both must have the same direction as well as magnitude.

1654753334271

Unit Vector: It is a vector that has a unit magnitude. Generally, it is used to show the direction of the vector. Conventionally three-unit vectors namely $\hat{i}, \hat{j}, and \ \hat{k}$ are used in the direction of the x-axis, y-axis, and z-axis.

The unit vector can be calculated by dividing the vector by its magnitude and represented as mentioned below.

$\hat{a} = \frac{\vec{a}}{|\vec{a}|}$

Vectors Addition Rules

Triangle Rule

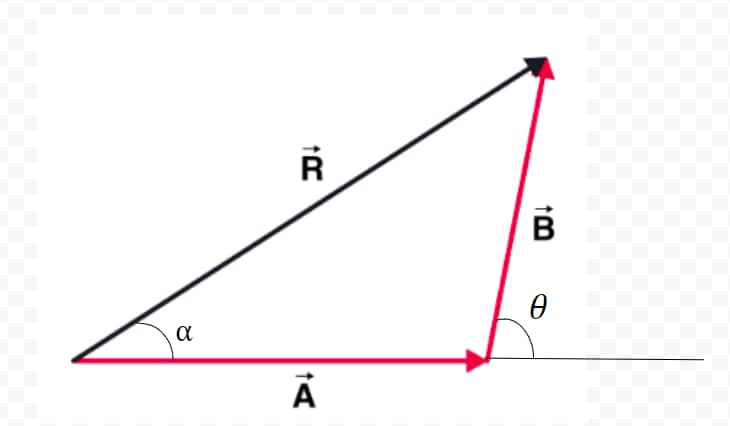
1654753331095

Let us consider two vectors and represented by two sides of a triangle, the head of is connected with the tail of as shown above in the image, then the third side in the opposite direction represents the resultant sum of these two vectors. Mathematically the resultant of two vectors can be calculated by the given formula.

$|\vec{A} + \vec{B}| = \sqrt{A^2+B^2+2ABcos \theta}$

$tan \alpha = \frac{Bsin\theta}{A+Bcos\theta}$

Where angle ⍺ is the angle between the resultant R vector and . ? is the angle between and . Remember that angle between two vectors can only be calculated when both vectors are connected head to head or tail to tail.

Parallelogram Rules

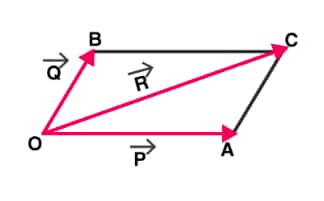
1654753331575

Let's consider two adjacent sides of a parallelogram represent two vectors and . As mentioned above in the diagram, the diagonal joining the intersecting point to the other corner of the parallelogram represents the resultant sum of vectors as shown in the image.

Subtraction And Addition Of Vectors

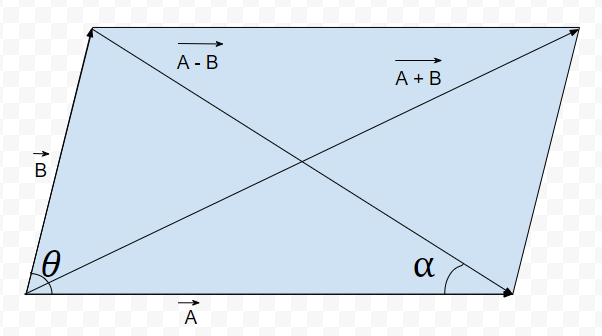
1654753329173

Subtraction of the vector is nothing but the addition of the negative vector to the other vector. Keeping the same magnitude and reversing the direction of a vector gives a negative vector. In a Parallelogram, one diagonal shows the addition of vectors, and the other one shows the subtraction of vectors as shown above in the figure.

Mathematical formula of subtraction of two vectors and

$|\vec{A} - \vec{B}| = \sqrt{A^2+B^2-2ABcos \theta}$

$tan \alpha = \frac{Bsin\theta}{A-Bcos\theta}$

Where ? is the angle between and and angle ? is between resultant vector $\vec{A} - \vec{B}$ and

Multiplication Of Vectors

Multiplication of vectors can be of two types: scalar vector multiplication and vector-vector multiplication. If we multiply a vector with a scalar quantity “k”, when “k” is positive, the direction remains the same and magnitude becomes “k” times, and when “k” is negative, magnitude becomes “k” time, but the direction gets reversed.

Vector multiplication is two types i.e dot product or scalar product and cross product or vector product which are explained below.

Dot Product

It is also called a scalar product, represented as (.) between two vectors. Dot product physically represents the multiplication of the magnitude of one vector with a component of another vector in the direction of the vector.

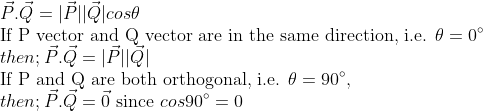
$\\ \vec{P}.\vec{Q} = |\vec{P}| |\vec{Q}| cos \theta \\ \text{If P vector and Q vector are in the same direction, i.e. } \theta = 0 {\degree} \\ then; \vec{P}.\vec{Q} = |\vec{P}| |\vec{Q}| \\ \text{If P and Q are both orthogonal, i.e. } \theta = 90 \degree , \\ then; \vec{P}.\vec{Q} = \vec{0} \ \text{since } cos 90 \degree = 0 \\$

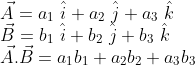
$\\ \vec{A} = a_{1} \ \hat{i}+a_{2} \ \hat{j}+a_{3} \ \hat{k} \\ \vec{B} = b_{1} \ \hat{i}+b_{2} \ \hat{j}+b_{3} \ \hat{k} \\ \vec{A}.\vec{B} = a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}$

Cross Product

Cross product is also known as the vector product is represented by the “X” sign between two vectors. If and are two vectors.

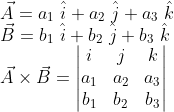
$\\ \vec{A} = a_{1} \ \hat{i}+a_{2} \ \hat{j}+a_{3} \ \hat{k} \\ \vec{B} = b_{1} \ \hat{i}+b_{2} \ \hat{j}+b_{3} \ \hat{k} \\ \vec{A} \times \vec{B} = \begin{vmatrix} i & j & k\\ a_{1} & a_{2} & a_{3}\\ b_{1}& b_{2} & b_{3} \end{vmatrix}$

Recommended eBooks

Related eBooks & Sample Papers

NEET vs NCERT Syllabus 2026: Common Chapters, Deleted Topics & Study Map (Free PDF)

3899+ Downloads

Top 50 Must-Practice NEET Physics Numericals with Solutions – Free PDF to Target 120+ Marks

2332+ Downloads

Other Important Formulas

$\hat{a} = \frac{\vec{a}}{|\vec{a}|}$

NEET Syllabus: Subjects & Chapters

Select your preferred subject to view the chapters

Logarithmic

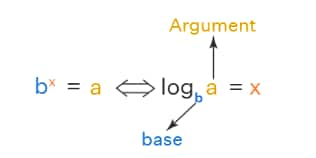
Logarithmic Function is an inverse function of exponential function which is defined as

x = log_ba, for b > 0, a > 0, and b ≠ 1, if and only if a = b^x. Generally, we come across two types of bases while solving NEET problems. That is 10 and the mathematical constant “e”. When the base is “e” it is called a natural logarithmic function and when the base is 10 then it is called a common logarithmic function.

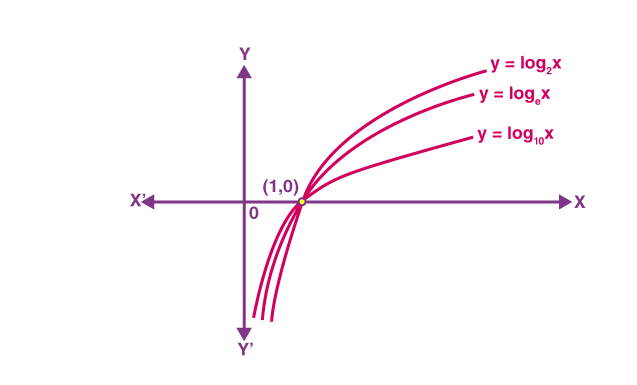
Natural logarithmic function f(x) = log_e x

Common logarithmic function f(x) = log₁₀ x

Logarithmic Function

1654753331731

Logarithmic Table

x	Base = 10 Log₁₀ x	Base = e ≈ 2.71; Log_e x
1	0	0
2	0.3010	0.693147
3	0.4771	1.098612
4	0.6020	1.386294
5	0.6989	1.609438
6	0.7781	1.791759
7	0.8450	1.94591
8	0.9030	2.079442
9	0.9542	2.197225
10	1	2.302585

Graph

1654753330769

Properties

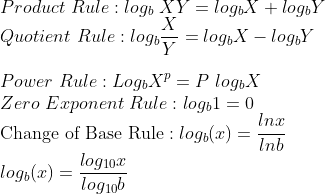
1654753331425

Exponential

It is a mathematical function that is used to find exponential decay and exponential growth of many real-life events like population models, radioactive decay, wounds healing models, and many more. Mathematically defined by a function f (x) = a.b^x, where “x” is a variable that can be any real number, “a” is constant but can not be zero, and “b” is an also constant know as base of exponential function and it should be greater than zero and not equal to 1. And the most commonly used exponential bases are 10 and “e” which is approximately equal to 2.718. This article includes rules, formulas, graphs, etc of the exponential function.

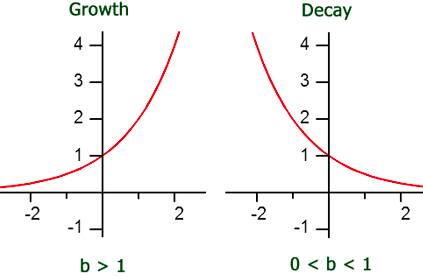
Exponential Growth

Initially, the quantity increases very slowly, and then rapidly. The rate of change increases over time. A mathematical expression that defines exponential growth is y = a ( 1+ r )^x where “ r ” is the growth percentage.

Exponential Decay

Initially, quantity decreases very rapidly, and then slowly. The mathematical expression to define exponential decay is y = a ( 1- r )^x where “ r ” is the decay percentage.

Exponential Growth And Decay Graph

1654753330406

Exponential And Logarithmic Function

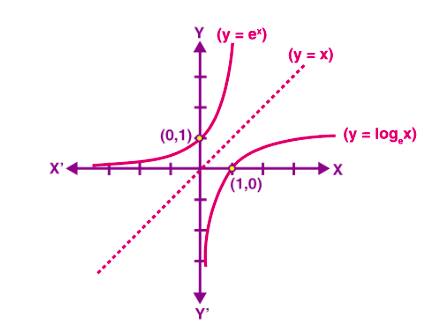
1654753330586

Exponential Function Rules

Following are some important rules that are repeatedly used. Here x and y are real numbers whereas “a” and “b” are positive numbers.

If a>0, and b>0, the following hold true for all the real numbers x and y:

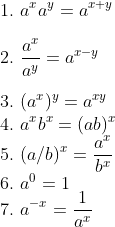
1654753329739

NEET Previous Five Years’ Analysis

Since the NEET exam is highly competitive, smart study can help students to succeed in the exam. Careers360 came up with an analysis to help them. The following list shows the number of questions in which vector algebra, exponential, and logarithmic concepts are used.

Numbers Of Questions Asked In Previous Five Years NEET Exam

	Vector Algebra	Exponential	Logarithmic
2021	4	2	1
2020	1	2	2
2019	5	2	1
2018	4	1	1
2017	1	3	1

Previous Years Questions To Understand The Concepts

Here is a list of previous year's questions with step-by-step explanations to understand vector algebra, exponential, and logarithmic concepts. NEET aspirants can develop an understanding of the level of questions along with the spread and depth of the concepts.

Q.1 NEET - 2021

In the product

What will be the complete expression for

Solution:

$\bar{F}=q\left ( \bar{v}\times \bar{B} \right )=q\bar{v}\times \left ( B\hat{i}+B\hat{j}+B_{0}\hat{k} \right )$ $\left [ 4\hat{i}-20\hat{j}+12\hat{k} \right ]=\left [ 2\hat{i}+4\hat{j}+6\hat{k} \right ]\times \left [ B\hat{i}+B\hat{j}+B_{0}\hat{k} \right ]$

$=\hat{i}\left ( 4B_{0}-6B \right )-\hat{j}\left ( 2B_{0}-6B \right )$ $+\hat{k}\left ( -2B \right )$

$4B_{0}-6B=4$

$2B_{0}-6B=20$

$2B_{0}=-16,B_{0}=-8$

$\bar{B}=B\hat{i}+B\hat{j}+B_{0}\hat{K}$

$\bar{B}=-6\hat{i}-6\hat{j}-8\hat{k}$

Concepts used:

Cross product formula:

Q.2. NEET - 2020

Find the torque about the origin when a force of $3\hat j N$ acts on a particle whose position vector is $2\hat k m$

Solution:

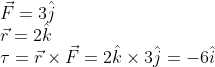
$\\ \vec{F}=3 \hat{j}\\ \vec{r}=2 \hat{k}\\ \tau =\vec{r}\times \vec{F}=2 \hat{k}\times 3 \hat{j}=-6 \hat{i}$

Concepts used:

Cross product formula:

Q.3. NEET - 2021

If force [F], acceleration [A], and time [T] are chosen as the fundamental physical quantities. find the dimensions of energy.

Solution:

$[Energy ]=[F]^{x}[A]^{y}[T]^{Z}$

$\left[M^{1} L^{2} T^{-2}\right]=\left[M^{1} L^{1} T^{-2}\right]^{x}[L^{1}T^{-2}]^{y}[T^{1}]^{z}$

$\left[M^{1} L^{2} T^{-2}\right]=M^{x} L^{x+y} T^{-2 y-2 x+z}$

Concepts Used:

1654753329618

Q.4. NEET - 2020

The rate constant for a first-order reaction is $4.606 \times 10^{-3}s^{-1}$ The time required to reduce 2 g of the reactant to 0.2 g is:

Solution:

We have given $K=4.606 \times 10^{-3}s^{-1}$ Thus, the reaction is of the first order. $\mathrm{K\: t\: =\: ln\frac{A_{o}}{A}}$

$\mathrm{4.606\: x\: 10^{-3}\: t\: =\: 2.303log\left (\frac{2}{0.2} \right )}$

Thus,

$\text {t}=500\; \text {sec}$

Concepts Used:

Log₁₀ 10 = 1

Q.5 NEET - 2020

The slope of the Arrhenius Plot $\left(\ln \mathrm{k\ v} / \mathrm{s}\ \frac{1}{\mathrm{T}}\right)$ of a first-order reaction is $-5 \times 10^{3} K$ . The value of of the reaction is. Choose the correct option for your answer.

Solution:

We know the Arrhenius equation

$\mathrm{k}=\mathrm{Ae}^{-\mathrm{E}_{\mathrm{a}} / \mathrm{RT}}$

$\ln \mathrm{k}=\ln \mathrm{A}+\ln \mathrm{e}^{-\mathrm{E}_{\mathrm{a}} / \mathrm{RT}}$

$\mathrm{\ln k=\ln A-\frac{E_{a}}{R}\left(\frac{1}{T}\right)}$

The slope of $\left(\ln \mathrm{k\ v} / \mathrm{s}\ \frac{1}{\mathrm{T}}\right)$ of the above equation -

$\mathrm{m=-\frac{E_{a}}{R}}$

Given, m = $-5 \times 10^{3} \mathrm{~K}$ and $\mathrm{R}=8.314 \mathrm{JK}^{-1} \mathrm{~mol}^{-1}$

$\mathrm{-5 \times 10^{3}=-\frac{E_{a}}{8.314}}$

$\mathrm{E_{a}=5 \times 10^{3} \times 8.314 \mathrm{~J} / \mathrm{mol}}$

$\mathrm{E_{a} =41.57 \times 10^{3} \mathrm{~J} / \mathrm{mol}}$

$\mathrm{E_{a}\simeq 41.5 \mathrm{~kJ} / \mathrm{mol}}$

Concepts Used:

Using property ln x^p = p ln x, simplify the equation and ln e = 1.

After going through this article it is clear that the NEET exam does not go deeper and asks just formula-based and simple concept-based questions. Therefore, even without mastering complex formulas and concepts of vector algebra students can score well in the exam. With continuous practice, aspirants can get command of the concepts.

Articles

IPU NEET Counselling 2025: Stray Round Seat Allotment Result (Out), Reporting, Joining

1 day ago

Counselling

CMC Vellore NEET Counselling 2025: Seat Allotment Result (Declared), Allotment Letter (November 20)

2 days ago

Counselling

CMC Vellore NEET Merit List 2025 (Out)- Download CMC Vellore Rank List PDF Here

2 days ago

Counselling

IPU NEET Merit List 2026 - Download IPU MBBS Merit List PDF

2 days ago

Counselling

Upcoming Medicine Exams

Odisha BSc Nursing

Ongoing Dates

Odisha BSc Nursing Counselling Date

1 Jan'26 - 15 Jan'26 (Online)

Result

Exam Pattern

Admit Card

Maharashtra Bachelor of Science in Nursing Common Entrance Test

Upcoming Dates

MH BSc Nursing CET Exam Date

6 May'26 - 7 May'26 (Online)

Admit Card

Exam Pattern

Result

All India Institute of Medical Sciences Paramedical Exam

Upcoming Dates

AIIMS Paramedical Exam Date

30 May'26 - 30 May'26 (Online)

Certifications By Top Providers

Biomolecules Structure Function in Health and Disease

Via All India Institute of Medical Sciences New Delhi

Industrial Biotechnology

Via Indian Institute of Technology Kharagpur

Certificate Course in Biostatistics, Epidemiology and Research Methodology

Via Manipal Academy of Higher Education, Manipal

Nutrition in the Health Sector

Via The University of Adelaide, Adelaide

Pathology

Via Tsinghua University, Beijing

Online M.Sc Psychology

Via Centre for Distance and Online Education, Andhra University

355 courses

310 courses

233 courses

191 courses

106 courses

Johns Hopkins University, Baltimore

75 courses

Biology and Life Sciences

Health, Fitness and Medicine

Psychology

Health Care Management

Explore Top Universities Across Globe

University College London, London

Gower Street, London, WC1E 6BT

University of Essex, Colchester

Wivenhoe Park Colchester CO4 3SQ

University of Nottingham, Nottingham

University Park, Nottingham NG7 2RD

University of Wisconsin, Madison

329 Union South 1308 W. Dayton Street Madison, WI 53715-1149

University of Alberta, Edmonton

116 St. and 85 Ave., Edmonton, Alberta, Canada T6G 2R3

Keele University, Newcastle

Staffordshire, UK, ST5 5BG

General Medicine and Surgery

Bio-Chemistry

Top Engineering Colleges in Germany - Check List, How to apply, Fees

11 min ⋆ Nov 28, 2025 07:11 AM IST

MBA in Italy for Indian Students 2026: Fees, Colleges, Requirements

6 min ⋆ Nov 28, 2025 04:11 AM IST

Proof of Funds List for Germany Student Visa in 2026

5 min ⋆ Nov 28, 2025 04:11 AM IST

Universities in Canada with No Application Fee for International Students 2026

5 min ⋆ Nov 28, 2025 04:11 AM IST

Intakes in Canada 2026 (Fall, Winter & Summer): How to Apply

5 min ⋆ Nov 27, 2025 04:11 AM IST

Study MBBS in Russia 2026: MBBS Fees, Colleges & Requirements

19 min ⋆ Nov 27, 2025 04:11 AM IST

Popular Courses and Specializations

Popular Degrees

Popular Branches

List of colleges accepting NEET

All India Institute of Medical Sciences New Delhi

Courses & FeesCut-offsAdmissionsPlacementsReviews

All India Institute of Medical Sciences Rishikesh

Courses & FeesCut-offsAdmissionsPlacementsReviews

Christian Medical College, Vellore

Courses & FeesCut-offsAdmissionsPlacementsFacilities

Atal Bihari Vajpayee Institute of Medical Sciences and Dr Ram Manohar Lohia Hospital, New Delhi

Courses & FeesCut-offsAdmissionsPlacementsFacilities

Ayurved Mahavidyalaya and Seth R V Ayurved Hospital, Mumbai

Courses & FeesCut-offsAdmissionsFacilitiesQues. & Ans

Ashtang Ayurved Mahavidyalaya, Pune

Courses & FeesCut-offsAdmissionsFacilitiesQues. & Ans

Browse Medicine Colleges by State

Maharashtra

Uttar Pradesh

Karnataka

Tamil Nadu

Kerala

Telangana

Questions related to NEET

On Question asked by student community

Have a question related to NEET ?

What other options do pcb students have besides neet and cuet

Hi there,

Apart from NEET and CUET you can explore the following career paths to

Students pursuing the PCB (Physics, Chemistry, Biology) stream can explore a wide range of options apart from CUET and NEET. Their choices are not just limited to medicine and can expand to include numerous areas

Read Complete Answer

Avartana Chauhan

7 Jan'26

Neet pervious 5 years question paper with solution pdf(2021-2025) free download

Hello,

The link to the papers is attached here. Solving previous year questions will help you understanding the important topics. You can also practice the sample papers and mock test papers of careers360 which will help you analyse your in-depth performance.

https://medicine.careers360.com/download/sample-papers/neet-previous-5-years-question-papers-20212025-answer-keys-solutions-pdf-free-download

Thank you.

Read Complete Answer

SUANGANA ROY

7 Jan'26

Neet question paper into Hindi

HELLO,

Below i am attaching the link through which you can download the NEET question paper in Hindi PDF

Here is the link :- https://medicine.careers360.com/hi/articles/neet-question-paper

Hope this will help you!

Read Complete Answer

Devanshi Goyal

7 Jan'26

Can you give the timetable for neet aspirarant to complete the syallbus within 4 months

Hello Akanksha

It is possible to complete the syllabus within 4 months with discipline and clear plan. You need to be consistent everyday.

•In the first month you can complete

Units & measurement, motion in 1d and 2d, laws of motion, work power energy

Some basic concepts of chemistry, atomic

Read Complete Answer

Ritika Tiwari

6 Jan'26

When will the application process will start for NEET registration in karnataka, Gujrat, maharashtra and Puduchery

Hello,

The application process for NEET UG 2026 state quota seats in Karnataka, Gujarat, Maharashtra, and Puducherry is expected to begin in July 2026, after the NEET 2026 results are announced in June 2026. The exact dates are announced by each state's respective counselling authority.

I hope it will clear

Popular NEET Questions

Column I ( Salivary gland)		Column II ( Their location)
Parotids	I	Below tongue
Sub-maxillary / sub-mandibular	Ii	Lower jaw
Sub-linguals	Iii	Cheek

Option: 1

a(i), b(ii) , c(iii)

Option: 2

a(ii), b(i), c(iii)

Option: 3

a(i), b(iii), c(ii)

Option: 4

a(iii), b(ii), c(i)

Read Complete Answer

$Ethyl \; ester \xrightarrow[(excess)]{CH_{3}MgBr} P$

the product 'P' will be ,

Option: 1

Option: 2

Option: 3

$\left ( C_{2}H_{5} \right )_{3} - C- OH$

Option: 4

Read Complete Answer

	Valve name		Function
I	Aortic valve	A	Prevents blood from going backward from the pulmonary artery to the right ventricle.
II	Mitral valve	B	Prevent blood from flowing backward from the right ventricle to the right atrium.
III	Pulmonic valve	C	Prevents backward flow from the aorta into the left ventricle.
IV	Tricuspid valve	D	Prevent backward flow from the left ventricle to the left atrium.

Option: 1

I – A , II – B, III – C, IV – D

Option: 2

I – B , II – C , III – A , IV – D

Option: 3

I – C , II – D , III – A , IV – B

Option: 4

I – D , II – A , III – B , IV – C

Read Complete Answer

Column A	Column B
A	a) Organisation of cellular contents and further cell growth.
B	b) Leads to formation of two daughter cells.
C	c) Cell grows physically and increase volume proteins,organells.
D	d) synthesis and replication of DNA.

Match the correct option as per the process shown in the diagram.

Option: 1

1-b,2-a,3-d,4-c

Option: 2

1-c,2-b,3-a,4-d

Option: 3

1-a,2-d,3-c,4-b

Option: 4

1-c,2-d,3-a,4-b

Read Complete Answer

0.014 Kg of N₂ gas at 27 ⁰C is kept in a closed vessel. How much heat is required to double the rms speed of the N₂ molecules?

Option: 1

3000 cal

Option: 2

2250 cal

Option: 3

2500 cal

Option: 4

3500 cal

Read Complete Answer

0.16 g of dibasic acid required 25 ml of decinormal $NaOH$ solution for complete neutralisation. The modecular weight of the acid will be

Option: 1

Option: 2

Option: 3

128

Option: 4

256

Read Complete Answer

0.5 F of electricity is passed through 500 mL of copper sulphate solution. The amount of copper (in g) which can be deposited will be:

Option: 1

31.75

Option: 2

15.8

Option: 3

47.4

Option: 4

63.5

Read Complete Answer

0.5 g of an organic substance was kjeldahlised and the ammonia released was neutralised by 100 ml 0.1 M HCl. Percentage of nitrogen in the compound is

Option: 1

Option: 2

Option: 3

Option: 4

Read Complete Answer

0xone is

Option: 1

$\mathrm{KO}_{2}$

Option: 2

$\mathrm{Na}_{2} \mathrm{O}_{2}$

Option: 3

$\mathrm{Li}_{2} \mathrm{O}$

Option: 4

$\mathrm{CaO}$

Read Complete Answer

(1) A substance known as "Smack"

(2) Diacetylmorphine

(3) Possessing a white color

(4) Devoid of any odor

(5) Crystal compound with a bitter taste

(6) Obtained by extracting from the latex of the poppy plant

The above statements/information are correct for:

Option: 1

Morphine

Option: 2

Heroin

Option: 3

Cocaine

Option: 4

Barbiturates

Read Complete Answer

Begin a career in Medical and Allied Sciences. Admissions Open for

JSS University Mysore 2025

Apply

NAAC A+ Accredited| Ranked #24 in University Category by NIRF | Applications open for multiple UG & PG Programs

Amity University-Noida Health and Allied Sciences Admissions

Apply

Amongst top 3% universities globally (QS Rankings) | Wide Range of scholarships available

View all Application Forms

NEET Notifications

NCAHP notifies UGC: NEET UG must for physiotherapy, university tests for psychology courses

Musab Qazi

Jan 10, 2026

NEET UG 2026 LIVE: NTA NEET syllabus out at neet.nta.nic.in; NEET brochure expected soon, updates

Durva Gupta

Jan 10, 2026

Punjab NEET PG round 3 registration deadline extended to January 8 for MD, MS

Sundararajan

Jan 07, 2026

MBBS admission criteria cannot be altered mid-process: SC slams Punjab govt

Press Trust of India

Jan 06, 2026

Chhattisgarh NEET PG Counselling 2025: Round 2 merit list out; 805 shortlisted for MD, MS admissions

Sundararajan

Jan 06, 2026

NEET UG 2026: NTA asks aspirants to update Aadhaar, UDID, category details before registration

Vaishnavi Shukla

Jan 05, 2026

Kerala NEET PG Counselling 2025: Round 3 option registration begins; allotment results on January 13

Sundararajan

Jan 05, 2026

Latest updates

NEET 2026 Syllabus (Released): Download Official PDF, Subjects, Chapters & Topics

Jan 08, 2026

Gujarat NEET Counselling 2025: Special Stray Round Seat Allotment Result (Out)

Jan 08, 2026

Biotechnology NEET Previous Year Questions with Answers & Analysis (2021–2025)

Jan 08, 2026

IPU NEET Counselling 2025: Stray Round Seat Allotment Result (Out), Reporting, Joining

Jan 08, 2026

IPU NEET Application Form 2025 (Released) For Phase 2- Direct Link to apply for MBBS/BDS

Jan 08, 2026

View all

Explore Career Options

By Industry

Orthotist and Prosthetist

Orthotists and Prosthetists are professionals who provide aid to patients with disabilities. They fix them to artificial limbs (prosthetics) and help them to regain stability. There are times when people lose their limbs in an accident. In some other occasions, they are born without a limb or orthopaedic impairment. Orthotists and prosthetists play a crucial role in their lives with fixing them to assistive devices and provide mobility.

6 Jobs Available

Pathologist

A pathologist is required to examine body fluids, tissues, and organs with the help of laboratory tests and microscopic examinations. Pathologists often work in hospitals and diagnostic labs, often assisting doctors when it comes to treatment decisions. Due to the increased demand for diagnostic services, pathology offers good career opportunities in clinical practices, research and academics.

5 Jobs Available

Veterinary Doctor

A Veterinarian is responsible for diagnosing, treating, and preventing diseases in animals. The individual performs surgeries, guides nutrition, and provides animal care. A Bachelor’s in Veterinary Science (B.Vsc.) is a mandatory degree. The profession brings together medical knowledge and a strong commitment to animal welfare.

5 Jobs Available

Speech Therapist

A Speech Therapist (Speech-Language Pathologist) diagnoses and treats speech, language, communication, and swallowing disorders across all ages. They work in hospitals, schools, clinics, and more. Becoming an SLP requires a master’s degree, clinical training, and certification. With rising demand, the career offers rewarding opportunities in therapy, education, and research.

4 Jobs Available

Gynaecologist

A gynaecologist is a medical specialist in women’s reproductive health, handling issues like menstruation, fertility, pregnancy, and childbirth. They perform exams, surgeries, and offer family planning services. To become one, students must complete MBBS and postgraduate training. Gynaecologists work in hospitals or clinics and are in high demand, with salaries growing significantly with experience.

4 Jobs Available

Audiologist

The audiologist career involves audiology professionals who are responsible to treat hearing loss and proactively preventing the relevant damage. Individuals who opt for a career as an audiologist use various testing strategies with the aim to determine if someone has a normal sensitivity to sounds or not. After the identification of hearing loss, a hearing doctor is required to determine which sections of the hearing are affected, to what extent they are affected, and where the wound causing the hearing loss is found. As soon as the hearing loss is identified, the patients are provided with recommendations for interventions and rehabilitation such as hearing aids, cochlear implants, and appropriate medical referrals. While audiology is a branch of science that studies and researches hearing, balance, and related disorders.

3 Jobs Available

Oncologist

An oncologist is a medical doctor who diagnoses and treats cancer using chemotherapy, radiation, surgery, and other therapies. They work with a team to create treatment plans tailored to each patient. Specialisations include medical, surgical, radiation, pediatric, gynecologic, and hematologic oncology. Becoming an oncologist in India requires an MBBS and postgraduate studies in oncology.

3 Jobs Available

Biochemist

A biochemist studies the chemical processes within living organisms, combining chemistry and biology. They conduct experiments, analyse data, and develop products like drugs and vaccines. Biochemists work in labs, healthcare, research, and education. A degree in biochemistry or related fields is essential, with advanced roles often requiring higher degrees. They also ensure quality control and may teach or mentor others.

2 Jobs Available

Never miss NEET update

Get timely NEET updates directly to your inbox. Stay informed!

Student Community: Where Questions Find Answers

Ask and get expert answers on exams, counselling, admissions, careers, and study options.

Download Careers360 App

All this at the convenience of your phone

Regular Exam Updates
Best College Recommendations
College & Rank predictors
Detailed Books and Sample Papers
Question and Answers

Scan and download the app

Applications Open

NEET Mock Test

NEET Five-Year Analysis: Solving Vectors Algebra, Logarithmic, And Exponential Questions

Vectors Addition Rules

Triangle Rule

Parallelogram Rules

Subtraction And Addition Of Vectors

NEET

NEET AYUSH All India Counseling

Maharashtra MBBS/BDS Counselling

Arunachal Pradesh MBBS/BDS Admissions

NEET AYUSH All India Counseling

Government Ayurveda Medical College and Hospital, Mysore

Taranath Government Ayurvedic Medical College, Bellary

Maharashtra MBBS/BDS Counselling

GSMC Mumbai - Seth GS Medical College, Mumbai

LTMMC Mumbai - Lokmanya Tilak Municipal Medical College, Sion, Mumbai

Arunachal Pradesh MBBS/BDS Admissions

KGMU Lucknow - King George's Medical University, Lucknow

Dr R Ahmed Dental College and Hospital, Kolkata

NEET UG

BMCRI Bangalore - Bangalore Medical College and Research Institute, Bangalore

KMC Mangalore - Kasturba Medical College, Mangalore

Karnataka MBBS/BDS Counselling

BMCRI Bangalore - Bangalore Medical College and Research Institute, Bangalore

KMC Mangalore - Kasturba Medical College, Mangalore

UP MBBS/BDS Counselling

KGMU Lucknow - King George's Medical University, Lucknow

Dr Ram Manohar Lohia Institute of Medical Sciences, Lucknow

Gujarat MBBS/BDS Counselling

BJMC Ahmedabad - B J Medical College, Ahmedabad

GMERS Medical College and Hospital, Sola

Madhya Pradesh MBBS/BDS Counselling

Gandhi Medical College, Bhopal

Gajra Raja Medical College, Gwalior

Kerala MBBS/BDS Counselling

Government Medical College, Kozhikode

Government Medical College, Thiruvananthapuram

Tamil Nadu MBBS/BDS Counselling

MMC Chennai - Madras Medical College, Chennai

Stanley Medical College, Chennai

Telangana MBBS/BDS Counselling

Osmania Medical College, Hyderabad

ESIC Medical College, Hyderabad