Moment Of Inertia Of The Solid Cylinder MCQ - Practice Questions with Answers
Quick Facts
-
6 Questions around this concept.
Solve by difficulty
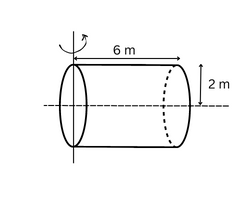
The moment of inertia of a uniform cylinder of length 6m and radius 2m about an axis perpendicular to its plane and passing through one of its ends is given by - [given mass of cylinder is 1kg]
Concepts Covered - 1
Let I= Moment of inertia of the CYLINDER about an axis through its center
To calculate I
Consider a cylinder of mass M, radius R, and length L.
mass per unit volume of the cylinder $\rho=\frac{M}{V}=\frac{M}{\pi R^2 L}$

Imagine that the cylinder is made of a large number of coaxial cylindrical shells
Take a small elemental cylindrical shell of mass dm having internal radius x and external radius (x + dx).
So for that elemental cylindrical shell $d V=(2 \pi x d x) L$
And
$$
d m=\rho d V=\frac{M}{\pi R^2 L}(2 \pi x d x) L
$$
$$
\Rightarrow d I=x^2 d m
$$
Now integrate this dI between the limits x=0 to x=R
$\begin{aligned} & I=\int d I=\int x^2 * \rho d v \\ & =\int_0^R \frac{M}{\pi R^2 L}\left(2 \pi * L x^3 d x\right) \\ & =\frac{2 M}{R^2} \int_0^R x^3 d x=\frac{M R^2}{2}\end{aligned}$
Study it with Videos
"Stay in the loop. Receive exam news, study resources, and expert advice!"


