Motion Of Two Bodies One Resting On The Other MCQ - Practice Questions with Answers

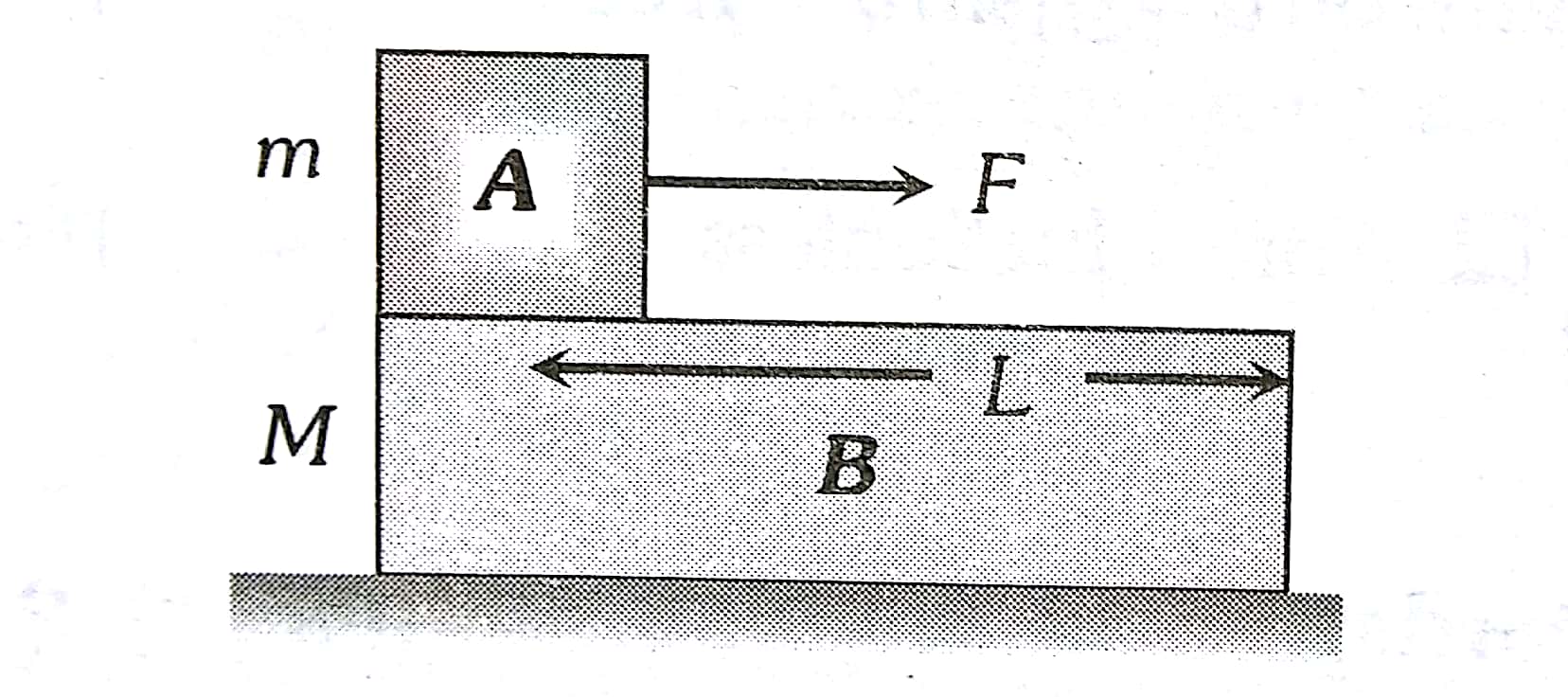
• Case1:- A force F is applied to the upper body, then the following four situations are possible:

1. When there is no friction:-

            Body A will move on body B with acceleration (F/m)

$
a_A=\frac{F}{m}
$

The body B will remain at rest

$
a_B=0
$

If $L$ is the length of $B$ as shown in the figure, $A$ will fall from $B$ after time,

$
t=\sqrt{\frac{2 L}{a}}=\sqrt{\frac{2 m L}{F}} \quad\left[\because s=\frac{1}{2} a t^2\right]
$
2.   If friction is present between A and B only and the applied force is less than limiting friction (F<F_l):-

                 (F = Applied force on the upper body, F_l = limiting friction between A and B, F_k = Kinetic friction between A and B)

                    Body A will not slide on body B till F<F_l i.e. F<μ_smg

               The combined system (m + M) will move together with common acceleration,

  $a_A=a_B=\frac{F}{m+M}$

3.    If friction is present between A and B only and the applied force is greater than limiting friction (F>f_l):-

In this condition, the two bodies will move in the same direction (i.e. of applied force) but with different acceleration. Here the force of kinetic friction μkmg will oppose the motion of A while causing the motion of B.

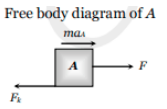
F-F_k=ma_A

i.e $a_A=\frac{F-F_k}{m}=\frac{F-\mu m g}{m}$

Similarly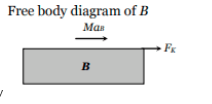 

$\begin{aligned} F_k & =M a_B \\ \text { i.e } a_B & =\frac{F_k}{M}=\frac{\mu m g}{M}\end{aligned}$

As both, bodies are moving in the same direction,

Acceleration of body A relative to B will be:

$
a=a_A-a_B=\frac{M F-\mu_k(m+M)}{m M}
$

So, A will fall from B after time,

$
t=\sqrt{\frac{2 L}{a}}=\sqrt{\frac{2 m M L}{M F-\mu_k m g(m+M)}}
$
 

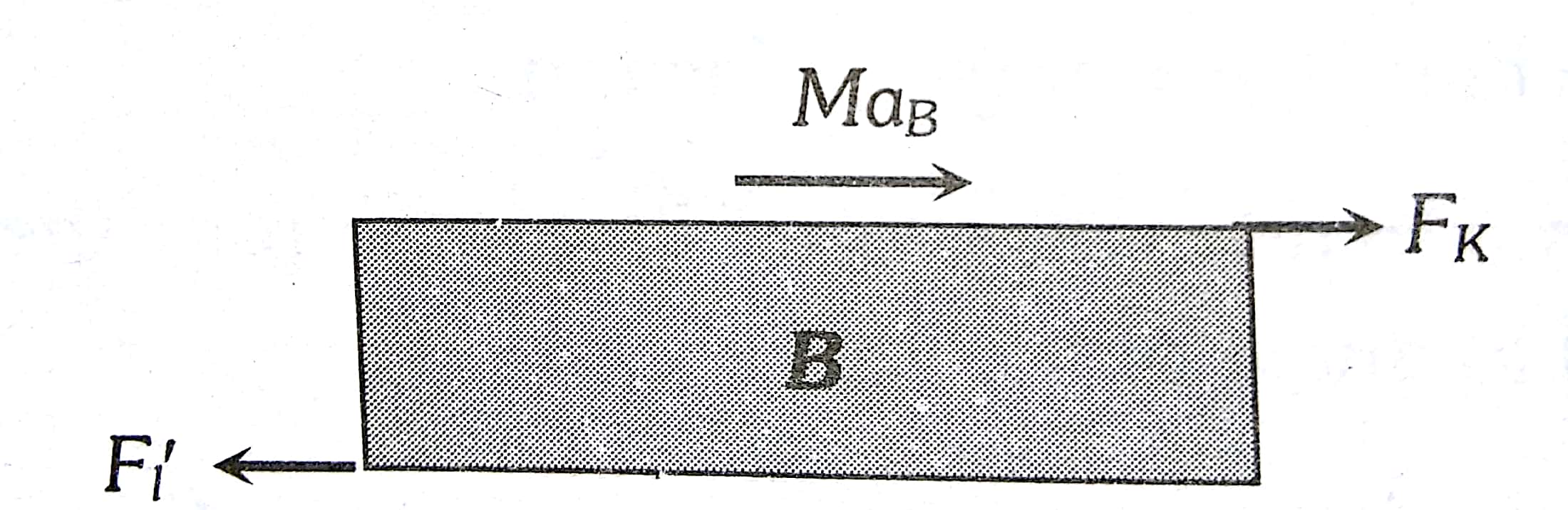
 4.    If there is friction between B and the floor:-

where

 $\left.F_l^{\prime}=\mu^{\prime}(M+m)\right) g$  equal to limiting friction between B and the floor.

and F_k=Kinetic friction between A and B

 B will move only if F_k>F’_l and then F_k-F’l=Ma_B

• Case 2:- A force F is applied to the lower body,

Let's discuss possible 4 situations in this case:-

1. When there is no friction:-

B will move with acceleration (F/M) while A will remain at rest (relative to ground) as there is no pulling force on A.

 $a_B=\frac{F}{M}$ and $a_A=0$

          As relative to B, A will move backward with acceleration (F/M) and so will fall from it in time t,

            $t=\sqrt{\frac{2 L}{a}}=\sqrt{\frac{2 M L}{F}}$

2.    If friction is present between A and B only and

            F' (Pseudo force on body A) < F_l (limiting friction between body A and B):-

                             Both the body will move together with common acceleration,

which is given by $a=\frac{F}{m+M}$
And the value of $F^{\prime}$ will be

$
\begin{aligned}
& \quad F^{\prime}=m a=\frac{F}{m+M}=\frac{m F}{m+M} \\
& \text { and } F_l=\mu_s m g \\
& \text { as } F^{\prime}<F_l \Rightarrow \frac{m F}{m+M}<\mu_s m g \\
& \left.\Rightarrow F<\mu_s(m+M)\right) g
\end{aligned}
$
  So both bodies will move together with acceleration, 

                             $a_A=a_B=\frac{F}{m+M}$ if $\left.F<\mu_s(m+M)\right) g$

3.     If friction is present between A and B only and F > F'_l(limiting friction between body A and B):-

               $\left.F_l^{\prime}=\mu_s(m+M)\right) g$

 Both the bodies will move with different accelerations. Here force of kinetic friction μkmg will oppose the motion of B while will cause the motion of A.

$\begin{aligned} & \quad m a_A=\mu_k m g \\ & \text { i.e } \quad a_A=u_k g\end{aligned}$

similarly

$\begin{aligned} F-F_k & =M a_B \\ \text { i.e. } \quad a_B & =\frac{\left[F-\mu_k m g\right]}{M}\end{aligned}$

As both, bodies are moving in the same direction,

Acceleration of body A relative to B will be given by:-

$a=a_A-a_B=-\left[\frac{F-\mu_k g(m+M)}{M}\right]$

              A negative sign implies that relative to B, A will move backward and will fall after time,

                   $t=\sqrt{\frac{2 L}{a}}=\sqrt{\frac{2 M L}{F-\mu_k g(m+M)}}$

 4.   If there is friction between B and floor and F>F_l''(limiting friction between body B and surface):-

Here $F_l^{\prime \prime}=\mu_s(m+M) g$
The system will move only if $\mathrm{F}>\mathrm{F}_{\text {, }}$ then replacing F by $F-F_l^{\prime \prime}$
The entire situation (3) will be valid.
However if

$
F<F_l^{\prime \prime} .
$
 

the system will not move.

This means friction between B and the floor will be F while between A and B is zero.