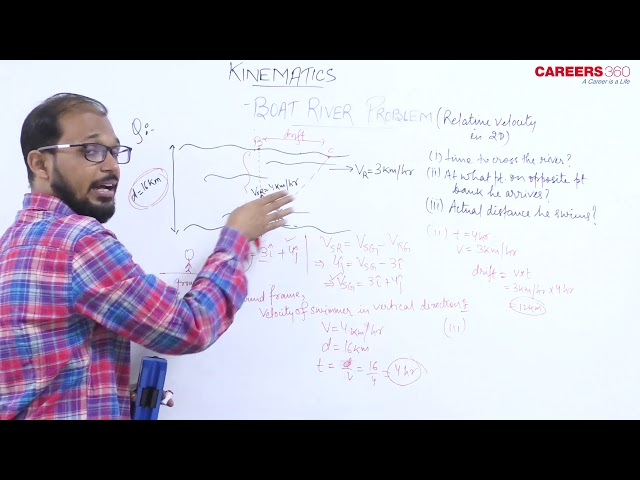
Boat River Problem MCQ - Practice Questions with Answers

1. Important terms

$d=$ width of river
$U=$ speed of river
$V=$ Speed of Boat w.r.t. River
and $V_b=$ Speed of boat w.r.t. Ground
Sa , the relation between $\mathrm{u} v$ and $V_b$ is

$$
V_b=U+V
$$

Let's try to find out $V_b$ in some important cases

   I)  When the boat travels downstream (u and v have the same direction)

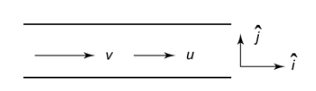
Then, $V_b=(U+V) \hat{i}$

II) When the boat travels upstream (u and v have opposite directions)

Then, $V_b=(U-V) \hat{i}$

III) If the boat travels at some angle with river flow (u)

        Now resolve v in two-component

Component of $\vee$ along $U=v_x=v \cos \theta \hat{i}$
Component of $\vee$ perpendicular to $U=v_y=v \sin \theta \hat{j}$
$\mathrm{So}_{\mathrm{o}} V_b=(v \cos \theta+u) \hat{i}+v \sin \theta \hat{j}$
and,

$$
\left|V_b\right|=\sqrt{u^2+v^2+2 u v \cos \theta}
$$

         Now if the time taken to cross the river is t

Then, $t=\frac{d}{v \sin \theta}$
Here $x=$ drift

And,

$$
x=(u+v \cos \theta) t=\frac{(u+v \cos \theta) d}{v \sin \theta}
$$

2. Important cases

    I) To cross the river in the shortest time

           This means v is perpendicular to u

or $\operatorname{Sin} \theta=1 \Rightarrow \theta=90^{\circ}$
So, $\left|V_b\right|=\sqrt{u^2+v^2}$

Time taken

$$
t_{\min }=\frac{d}{v}
$$

Drift along river flow,

$$
x=d\left(\frac{u}{v}\right)
$$
 

II) To cross the river in the shortest path

          Means drift = 0

$$
\begin{aligned}
& x=(u+v \cos \theta) t=0 \Rightarrow \cos \theta=\frac{-u}{v} \\
& \left|V_b\right|=\sqrt{v^2-u^2}
\end{aligned}
$$

Time taken to cross the river is

$$
\begin{aligned}
& t=\frac{d}{v \sin \theta} \\
& t=\frac{d}{\sqrt{v^2-u^2}}
\end{aligned}
$$