Mayer's Formula MCQ - Practice Questions with Answers

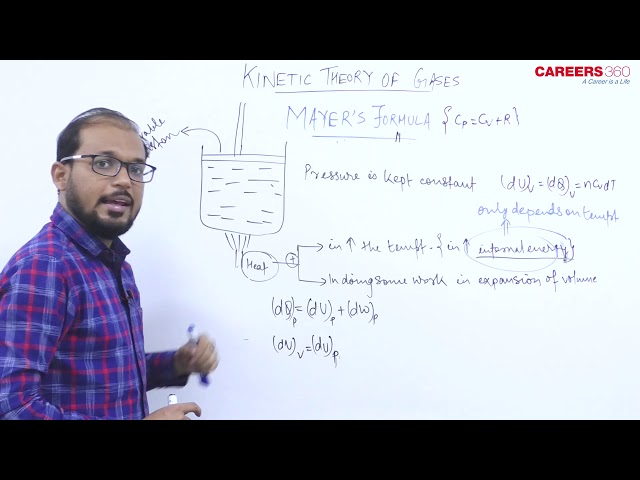
• Mayer's formula- As we know 

Molar Specific heat of the gas at constant volume $=C_v$ and Molar-specific heat capacity at constant pressure $=C_p$

Mayer's formula gives the relation between $C_p$ and $C_v$ as $C_p=C_v+R$ or we can say that molar Mayer's formula shows that specific heat at constant pressure is greater than that at constant volume.

• Specific Heat in Terms of Degree of Freedom

1. Molar Specific heat of the gas at constant volume $\left(C_{v)}\right.$

For a gas at temperature T , the internal energy

$$
U=\frac{f}{2} n R T \Rightarrow \text { Change in energy } \Delta U=\frac{f}{2} n R \Delta T \ldots \text { (i) }
$$

Also, as we know any gas heat supplied at a constant volume

$$
(\Delta Q)_V=n C_V \Delta T=\Delta U \ldots \ldots .(i i)
$$

From the equation (i) and (ii)

$$
C_v=\frac{f R}{2}
$$

where 

f = degree of freedom

R= Universal gas constant

2. Molar Specific heat of the gas at constant pressure $\left(C_p\right)$

From Mayer's formula, we know that $C_p=C_v+R$

$$
\Rightarrow C_P=C_V+R=\frac{f}{2} R+R=\left(\frac{f}{2}+1\right) R
$$

3. Atomicity or adiabatic coefficient $(\gamma)$

It is the ratio of $C_{p \text { to }} C_v$

$$
\gamma=\frac{C_p}{C_v}=1+\frac{2}{f}
$$

Value of $\gamma$ is always more than
for Monoatomic gas

$$
\gamma=\frac{5}{3}
$$

for Diatomic gas

$$
\gamma=\frac{7}{5}
$$

for Triatomic gas

$$
\gamma=\frac{4}{3}
$$

•  Gaseous Mixture

If two non-reactive gases A and B are enclosed in a vessel of volume V.

In the mixture $n_1$ mole of Gas A (having Specific capacities as $C_{p 1}$ and $C_{v 1}$. Degree of freedom $f_1$ and Molar mass as $M_{1 \text { ) is mixed with }}$
$\mathrm{n}_2$ mole of Gas B (having Specific capacities as $C_{p 2}$ and $C_{v 2}$. Degree of freedom $f_2$ and Molar mass as $M_{2 \text { ) }}$

Then Specific heat of the mixture at constant volume will be

$$
C_{v_{\operatorname{mix}}}=\frac{n_1 C_{v_1}+n_2 C_{v_2}}{n_1+n_2}
$$

Similarly, the Specific heat of the mixture at constant pressure will be

$$
C_{p_{\operatorname{mix}}}=\frac{n_1 C_{p_1}+n_2 C_{p_2}}{n_1+n_2}
$$

The adiabatic coefficient () of the mixture is given by

$$
\gamma_{\text {mixure }}=\frac{C_{p_{\text {mix }}}}{C_{v_{m x}}}=\frac{\frac{\left(n_1 C_{p_1}+n_2 C_{p_2}\right)}{n_1+n_2}}{\frac{\left(n_1 C_{v_1}+n_2 C_{v_2}\right)}{n_1+n_2}}=\frac{\left(n_1 C_{p_1}+n_2 C_{p_2}\right)}{\left(n_1 C_{v_1}+n_2 C_{v_2}\right)}
$$

Also

$$
\frac{1}{\gamma_{\text {mix }}-1}=\frac{\frac{n_1}{\gamma_1-1}+\frac{n_2}{\gamma_2-1}}{n_1+n_2}
$$

Similarly, the Degree of freedom of mixture is given as

$$
f_{m i x}=\frac{n_1 f_1+n_2 f_2}{n_1+n_2}
$$

Similarly, the molar mass of the mixture

$$
M_{\operatorname{mix}}=\frac{n_1 M_1+n_2 M_2}{n_1+n_2}
$$