Projectile On An Inclined Plane MCQ - Practice Questions with Answers

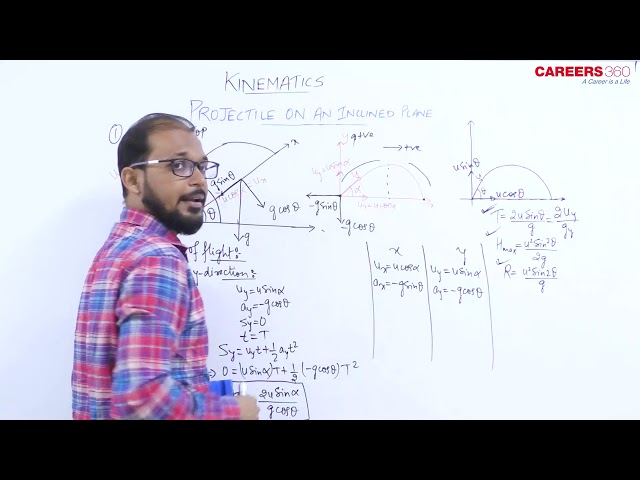
1. Important equations

                             U=Speed of projection

$\alpha=$ Angle of projection above-inclined plane (measured from the horizontal line)
$\theta=$ Angle of projection above-inclined plane (measured from an inclined plane)
$\beta=$ Angle of inclination.

   a) Initial Velocity- U

Component along $\times$ or along inclined plane $=U_x=U \cos \theta$
Component along y or perpendicular to inclined plane $=U_y=U \operatorname{Sin} \theta$

b) Final velocity $=V$

Component along $\times$ or along inclined plane $=V_x=U \cos \theta-(g \sin \beta) \cdot t$
Component along y or perpendicular to inclined plane $=V_y=U \sin \theta-(g \cos \beta) \cdot t$
and,

$$
V=\sqrt{V_x^2+V_y^2}
$$
 

    c) Displacement=S

Component along $\times$ or along inclined plane $=S_x=U_x t+\frac{1}{2} a_x \cdot t^2$ Component along y or perpendicular to inclined plane $=S_y=U_y t+\frac{1}{2} a_y \cdot t^2$

$$
\text { And } S=\sqrt{S_x^2+S_y^2}
$$

   d) Acceleration = a 

 Component along $\times$ or along inclined plane $=a_x=-g \sin \beta$
Component along y or perpendicular to inclined plane $=a_y=-g \cos \beta$
So $a=-g$

2. Important Terms

a) Time of flight

Formula

$$
T=\frac{2 U \sin \theta}{g \cos \beta}
$$

b) Range along incline plane

Formula

$$
R=\frac{2 u^2 \cdot \sin (\alpha-\beta) \cdot \cos \alpha}{g \cos ^2 \beta}
$$