Banking Of Road MCQ - Practice Questions with Answers

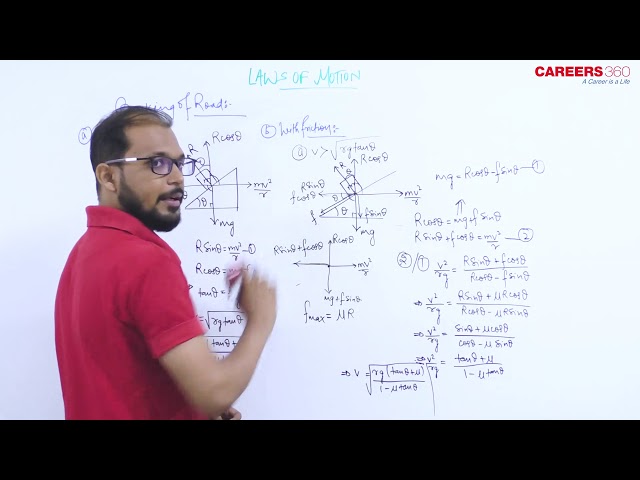
1. Without friction

From figure

$$
\begin{aligned}
& R \cos \theta=m g \\
& R \sin \theta=\frac{m v^2}{r} \\
& \tan \theta=\frac{v^2}{r g} \\
& \tan \theta=\frac{\omega^2 r}{g}=\frac{V \omega}{g}=\frac{h}{l}
\end{aligned}
$$

$h$ = height of outer edge from the ground level
$l=$ width of the road

r = radius

2.  If friction is also present

$$
\frac{V^2}{r g}=\frac{\mu+\tan \theta}{1-\mu \tan \theta}
$$

Where $\theta=$ angle of banking
$\mu=$ coefficient of friction
$V=$ velocity
Maximum speed on a banked frictional road

$$
V=\sqrt{\frac{r g(\mu+\tan \theta)}{1-\mu \tan \theta}}
$$