Calculation Of Necessary Force In Different Conditions On Rough Surface MCQ - Practice Questions with Answers

• Case 1:- Minimum pulling force P at an angle α from the horizontal

By resolving P in the horizontal and vertical direction, we get:

where F is the friction force.

For the condition of equilibrium,

$
\begin{aligned}
& F=P \cos \alpha \\
& R=W-P \sin \alpha
\end{aligned}
$
By substituting these values in $F=\mu R$, we get:

$
\begin{aligned}
& P \cos \alpha=\mu(W-P \sin \alpha) \\
& U \operatorname{se}=\mu=\tan \theta \\
& \Rightarrow P \cos \alpha=\frac{\sin \theta}{\cos \theta}(W-P \sin \alpha)
\end{aligned}
$
 

$P=\frac{W \sin \alpha}{\cos (\alpha-\theta)}$

    where P is the pulling force,

R is a normal reaction

W is the weight

• Case 2:- Minimum pushing force P at an angle α from the horizontal

By resolving P in the horizontal and vertical direction, we get:

      For the condition of equilibrium,

$
\begin{aligned}
& F=P \cos \alpha \\
& R=W+P \sin \alpha
\end{aligned}
$

By substituting the se values in $F=\mu R$, we get:

$
\begin{aligned}
& P \cos \alpha=\mu(W+P \sin \alpha) \\
& U s e=\mu=\tan \theta \\
& \Rightarrow P \cos \alpha=\frac{\sin \theta}{\cos \theta}(W+P \sin \alpha)
\end{aligned}
$
 

$P=\frac{W \sin \theta}{\cos (\alpha+\theta)}$

• Case 3:- Minimum pulling force P to move the body upwards on an inclined plane

          By resolving P in the direction of the plane and perpendicular to the plane, we get:

                     For the condition of equilibrium

$
\begin{aligned}
& R+P \sin \alpha=W \cos \lambda \Rightarrow R=W \cos \lambda-P \sin \alpha \\
& F+W \sin \lambda=P \cos \alpha \Rightarrow F=P \cos \alpha-W \sin \lambda
\end{aligned}
$

By substituting these values in $\mathrm{F}=\mu \mathrm{R}$, we get:

$
P=\frac{W \sin (\theta+\lambda)}{\cos (\alpha-\theta)}
$
 

• Case 4:- Minimum force to move a body in a downward direction along the surface of the inclined plane

         By resolving P in the direction of the plane and perpendicular to the plane, we get:

         For the condition of equilibrium,

$$
\begin{aligned}
& R+P \sin \alpha=W \cos \lambda \Rightarrow R=W \cos \lambda-P \sin \alpha \\
& F=P \cos \alpha+W \sin \lambda
\end{aligned}
$$

By substituting these values in $\mathrm{F}=\mu \mathrm{R}$, we get:

$$
P=\frac{W \sin (\theta-\lambda)}{\cos (\alpha-\theta)}
$$
 

• Case 5:- Minimum force to avoid sliding of a body down on an inclined plane

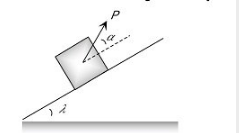
         By resolving P in the direction of the plane and perpendicular to the plane, we get:-

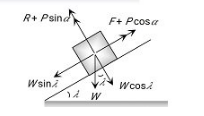
             For the condition of equilibrium,

$$
\begin{aligned}
& R+P \sin \alpha=W \cos \lambda \Rightarrow R=W \cos \lambda-P \sin \alpha \\
& F=W \sin \lambda-P \cos \alpha
\end{aligned}
$$

By substituting these values in $F=\mu R$, we get

$$
P=\frac{W \sin (\lambda-\theta)}{\cos (\theta+\alpha)}
$$
 

• Case 6:- Minimum Force of Motion along the horizontal surface and its direction

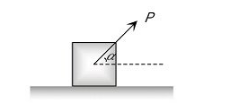
Let the force P be applied at an angle α with the horizontal.

By resolving P in horizontal and vertical direction, we get:-

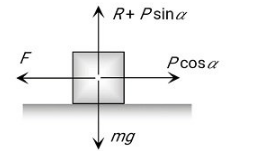
                  For vertical equilibrium,

$$
R+P \sin \alpha=m g \Rightarrow \therefore R=m g-P \sin \alpha
$$

and for horizontal motion,

$$
P \cos \alpha \geq F \Rightarrow P \cos \alpha \geq \mu R
$$

Substituting the value of $R$, we get:-

$$
\begin{aligned}
P \cos \alpha & \geq \mu(m f-P \sin \alpha) \\
\Rightarrow P & \geq \frac{\mu m g}{\cos \alpha+\mu \sin \alpha}
\end{aligned}
$$

For the force P to be minimum $(\cos \alpha+\mu \sin \alpha)$ must be maximum i.e.,

$$
\begin{aligned}
& \frac{\mathrm{d}}{\mathrm{~d} \alpha}[\cos \alpha+\mu \sin \alpha]=0 \\
& \Rightarrow-\sin \alpha+\mu \cos \alpha=0
\end{aligned}
$$

$$
\begin{aligned}
& \therefore \tan \alpha=\mu \\
& \Rightarrow \alpha=\tan ^{-1}(\mu)=\text { angle of friction. }
\end{aligned}
$$
 

             i.e. For the minimum value of P, its angle from the horizontal should be

             equal to the angle of friction.

                 $\tan \alpha=\mu$,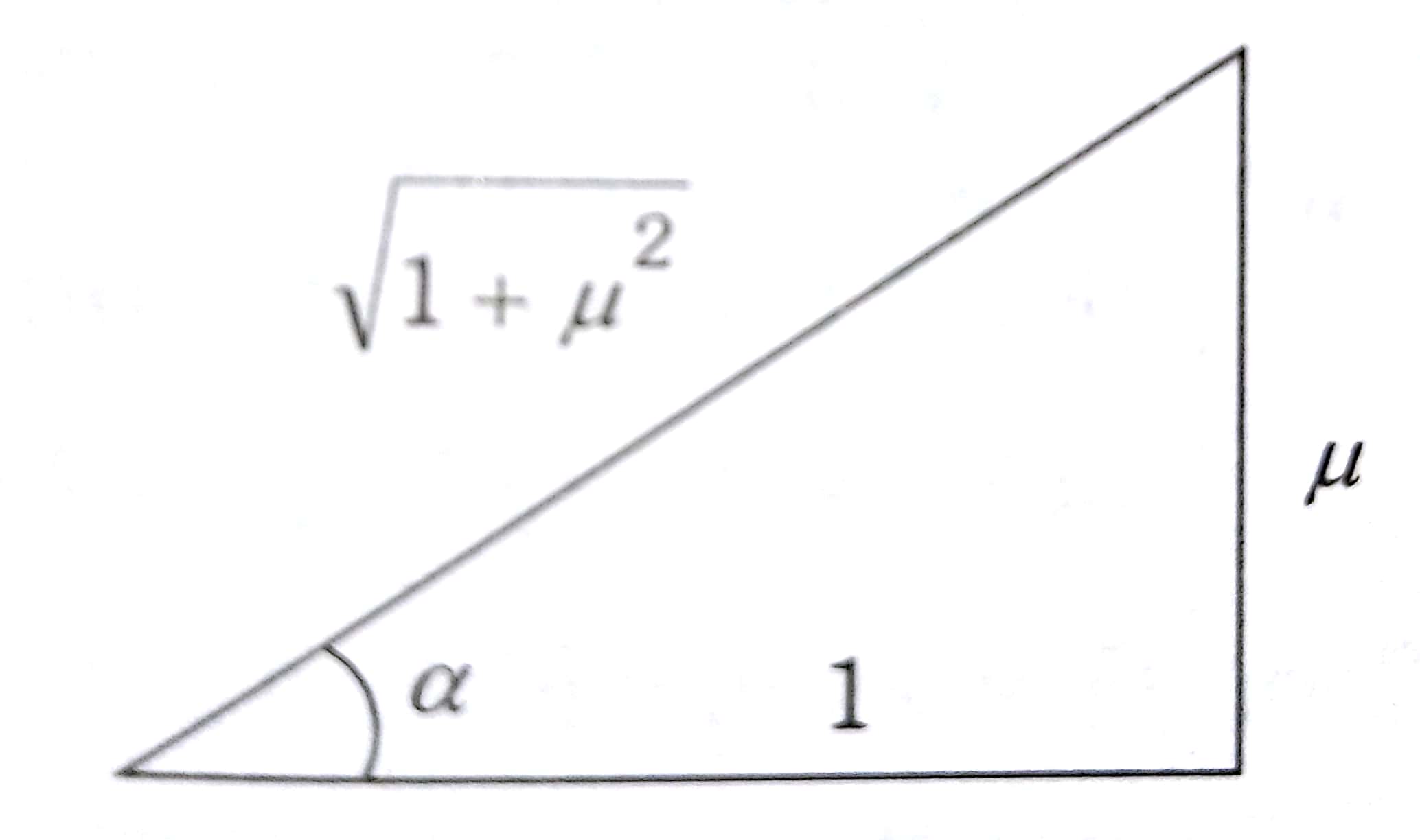

$$
\sin \alpha=\frac{\mu}{\sqrt{1+\mu^2}} \quad \operatorname{and} \quad \cos \alpha=\frac{1}{\sqrt{1+\mu^2}}
$$

By substituting these values,

$$
\begin{aligned}
& P \geq \frac{\mu m g}{\frac{1}{\sqrt{1+\mu^2}}+\frac{\mu^2}{\sqrt{1+\mu^2}}} \\
& \Rightarrow P \geq \frac{\mu m g}{\sqrt{1+\mu^2}} \\
& \therefore P_{\min }=\frac{\mu m g}{\sqrt{1+\mu^2}}
\end{aligned}
$$