Coefficient Of Friction Between A Body And Wedge MCQ - Practice Questions with Answers

• If the same wedge is made rough then the time taken by it to come down becomes n  times more (nt) 

Then find the Coefficient of Friction between the body and wedge in terms of n

For this make 2 cases

Case 1- A body slides on a smooth wedge of angle θ and its time of descent is t.

Case 2- If the same wedge is made rough then the time taken by it to come down becomes n times more (i.e., nt)

(The length of the path in both cases is the same)

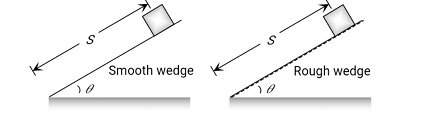
For smooth wedge

$
\begin{aligned}
& S=u \cdot t+\frac{1}{2} a t^2 \\
& S=\frac{1}{2}(g \sin \theta) t^2 \\
& \mathbf{u}=0 \\
& a=g \sin \theta
\end{aligned}
$

For Rough wedge

$
S=\frac{1}{2} g[\sin \theta-\mu \cos \theta](n t)^2
$

(i) $=$ (ii)

$
\mu=\tan \theta\left[1-\frac{1}{n^2}\right]
$

$\mu=$ coefficient of friction
$\theta=$ Angle of inclination
$\mathrm{n}=\mathrm{an}$ integer