Minimum Mass Hung From The String To Just Start The Motion MCQ - Practice Questions with Answers

 Here m₁ is connected to one end of the string and m₂ is connected to another end of the string. And mass m₂ hung from the string connected by the pulley,

Case 1:-

When a mass m₁ placed on a rough horizontal plane

So  the tension (T) produced in the string will try to start the motion of mass m₁:

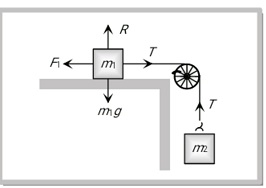
For liming condition

$
\begin{aligned}
& T=F_l \\
& m_2 g=\mu R \\
& m_2 g=\mu m_1 g
\end{aligned}
$

$m_2=\mu m_1=$ minimum value of $\mathbf{m}_2$ to start the motion

So $\mu=\frac{m_2}{m_1}$
where $\mathrm{T}=$ Tension in a string
$F_l=$ Limiting friction
$\mu=$ Coefficient of friction

• Case 2:-

      When a mass m₁ is placed on a rough inclined plane 

     So the tension (T) produced in the string will try to start the motion of mass m₁:

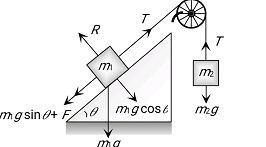
For limiting condition

For $m_2 \quad T=m_2 g$
For $m_1 \quad T=m_1 g \sin \theta+F$

$
T=m_1 g \sin \theta+\mu m_1 \cos \theta
$

Use (i) \& (ii)
$m_2=m_1[\sin \theta+\mu \cos \theta]=$ minimum value of $m_2$ to start the motion

where T = tension 

m₂ g = weigh of mass m₂

F = limiting friction

$
\text { Here } \mu=\left[\frac{m_2}{m_1 \cos \theta}-\tan \theta\right]
$

$\mu=$ coefficient of friction