Sticking Of A Block With Accelerated Cart MCQ - Practice Questions with Answers
Quick Facts
-
3 Questions around this concept.
Solve by difficulty
As shown here, in the figure, a cart C with mass M moving with acceleration 'b'. If the coefficient of friction between the block A having mass m and the cart is μ, then, acceleration of cart and block system is independent of:
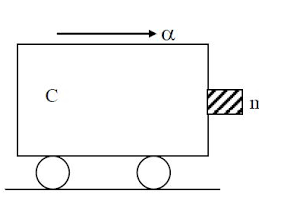
A block of mass m is in contact with the cart C as shown in the figure.
The coefficient of static friction between the block and the cart is $\mu$. The acceleration $\alpha$ of the cart that will prevent the block from falling satisfies
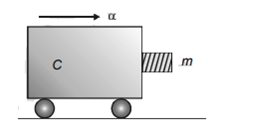
A block of mass m is in contact with cart C as shown in Figure:
.
The coefficient of static friction between the block and the cart is $\mu$. The acceleration $\alpha$ of the cart that will prevent the block from falling satisfies:
NEET 2026: Exam Centres List | Free NEET Coaching & Study Material
NEET Prep: Mock Test | 10 Years PYQ's | Syllabus
NEET 2026: Boards Cheat Sheet | Mind Maps & Diagrams Guide | Formula Sheet
Latest: Allied and Health Sciences | Paramedical Universities Accepting Applications
Concepts Covered - 1
While solving with the help of the concept of pseudo force.
When a cart moves with some acceleration toward right then a pseudo force (ma) acts on block toward left.
This force (ma) is an action force by a block on the cart.
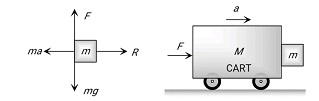
Now block will remain static w.r.t. block. If friction force= μR≥mg
For equilibrium condition
$$
\begin{aligned}
& \mu m a \geq m g \\
& a \geq \frac{g}{\mu}
\end{aligned}
$$
$$
\mathrm{R}=\mathrm{ma}
$$
$$
\begin{aligned}
\therefore & a_{\min }=\frac{g}{\mu} \\
& F_{\min }=(M+m) \frac{g}{\mu}
\end{aligned}
$$
Pseuda force (ma) acts on block towards left
$\mathrm{F}_{\text {min }}=$ Minimum force
$\mathrm{a}_{\text {min }}=$ minimum acceleration cart
$M_1 m$ are masses of the cart and block respectively
Study it with Videos
"Stay in the loop. Receive exam news, study resources, and expert advice!"