Stopping Of Block Due To Friction MCQ - Practice Questions with Answers

Case 1:-  On the horizontal road

  A block of mass m is moving initially with velocity u on a rough surface and due to friction, it comes to rest after covering a distance S.

•            Distance traveled before coming to rest (S):

$\begin{aligned} & F=m a=\mu R \\ & m a=\mu m g \\ & a=\mu g \\ & V^2=u^2-2 a s \\ & S=\frac{u^2}{2 \mu g}=\frac{P^2}{2 \mu m^2 g} \\ & \mathrm{a}=\text { acceleration } \\ & \mu=\text { coefficient of friction }\end{aligned}$

S = distance traveled

g = gravity

u=initial velocity

V = finally velocity

P=initial mometum=mu

•    Time taken to come to rest: 

From equation $v=u-a t \Rightarrow 0=u-\mu g t \quad[$ As $v=0, a=\mu g]$

$
\therefore t=\frac{u}{\mu g}
$

- Force of friction acting on the body:

$
\begin{aligned}
& F=m a \\
& F=m \frac{(v-u)}{t} \\
& F=\frac{m u}{t} \\
& F=\mu m g \quad[\text { As } v=0] \\
& {\left[\text { As } t=\frac{u}{\mu g}\right]}
\end{aligned}
$
 

Case 2:- On the inclined road :

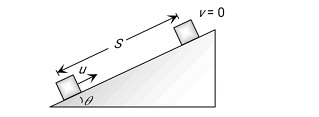
$\begin{aligned} & a=g[\sin \theta+\mu \cos \theta] \\ & V^2=u^2-2 a S \\ & 0=u^2-2 g[\sin \theta+\mu \cos \theta] S \\ & S=\frac{u^2}{2 g(\sin \theta+\mu \cos \theta)} \\ & \mathrm{S}=\text { distance traveled } \\ & \mu=\text { coefficient of friction } \\ & \mathrm{V}=\text { Final velocity } \\ & \mathrm{u}=\text { Initial velocity }\end{aligned}$