Kinematics Questions for NEET Previous Year Question Papers

Importance of Kinematics in the NEET 2026 Syllabus

Questions from kinematics range from basic formula-based problems to conceptual and graphical interpretations, such as position-time, velocity-time, and acceleration-time graphs.

Many students struggle with understanding motion graphs, vector decomposition, and applying equations of motion in different scenarios. However, solving NEET previous year questions (PYQs) effectively familiarises students with exam patterns, enhances problem-solving skills, and improves accuracy.

The unit comprises the major concepts given below:

NEET Kinematics PYQ Analysis: Frequency of Questions in the Last 5 Years

To help students understand the importance of Kinematics in NEET, we have compiled PYQs from 2020-2025, categorising them by sub-topic, difficulty level, and type of question.

Year-wise Distribution of PYQs (2020-2025)

Key Insights from the NEET Kinematics PYQ Analysis

• Equations of Motion and Projectile Motion are the most frequently asked topics.

• The difficulty level is moderate to high, with most questions being of medium difficulty.

• Conceptual and graphical questions dominate the unit.

• Relative Velocity and Vector Analysis are recurring topics in NEET PYQs.

Top Kinematics PYQs with Solutions for NEET 2026

Here are some of the most important PYQs from Kinematics, with detailed solutions.

Ques 1: If the magnitude of the sum of two vectors is equal to the magnitude of the difference of the two vectors, the angle between these vectors is:

Option 1: 0^o

Option 2: 90o

Option 3: 45^o

Option 4: 180^o

Difficulty level: Easy

Answer:

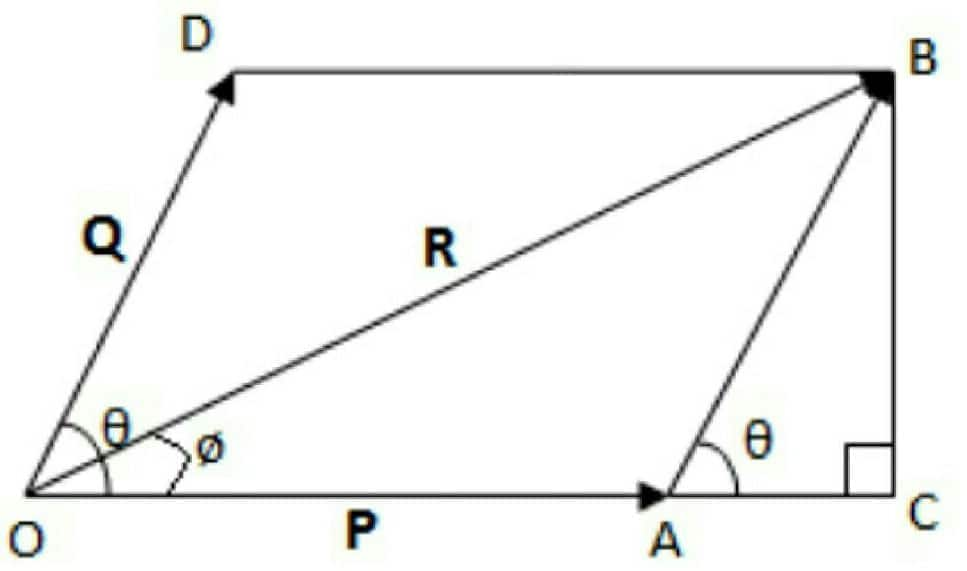
Represents the law of parallelogram vector addition:

\( |\vec{A} - \vec{B}| = |\vec{A} + \vec{B}| = \sqrt{A^2 + B^2 - 2AB\cos\theta} \)

Now using the given values:

\( A^2 + B^2 - 2AB\cos\theta = A^2 + B^2 + 2AB\cos(90^\circ) \)

Since \( \cos(90^\circ) = 0 \), we get \( 2AB\cos(90^\circ) = 0 \)

\( \Rightarrow |\vec{A} - \vec{B}| = \sqrt{A^2 + B^2} \)

So, the vectors are perpendicular:

\( \angle AB = 90^\circ \)

Hence, the answer is option (2).

Ques 2: A particle of mass 10 g moves along a circle of radius 6.4 cm with a constant tangential acceleration. What is the magnitude of this acceleration if the kinetic energy of the particle becomes equal to 8 x 10^-4 J by the end of the second revolution after the beginning of the motion?

Option 1: 0.1 m/s2

Option 2: 0.15 m/s2

Option 3: 0.18 m/s2

Option 4: 0.2 m/s2

Difficulty level: Medium

Answer:

Given:

Mass of particle, \( m = 10\,\text{g} = 10 \times 10^{-3}\,\text{kg} \)

Radius of circle, \( r = 6.4\,\text{cm} = 6.4 \times 10^{-2}\,\text{m} \)

Kinetic energy after 2 revolutions: \( KE = 8 \times 10^{-4}\,\text{J} \)

Let the constant tangential acceleration be \( a_t \).

Step 1: Total distance travelled in 2 revolutions

\( s = 2 \times 2\pi r = 4\pi r = 4 \times 3.14 \times 6.4 \times 10^{-2} = 8.0384\,\text{m} \)

Step 2: Using equation of motion

\( v^2 = 2a_t s \)

Using \( \frac{1}{2}mv^2 = \frac{1}{2}m(2a_t s) = KE \)

So, \( KE = m a_t s \Rightarrow a_t = \frac{KE}{ms} \)

\( a_t = \frac{8 \times 10^{-4}}{(10 \times 10^{-3}) \times 8.0384} = \frac{8 \times 10^{-4}}{8.0384 \times 10^{-2}} \approx 0.0995 \approx 0.1\,\text{m/s}^2 \)

Final Answer: Option 1) \( 0.1\,\text{m/s}^2 \)

Alternate verification:

Given \( KE = \frac{1}{2} mV^2 = 8 \times 10^{-4}\,\text{J} \)

Then \( V^2 = \frac{2 \times KE}{m} = \frac{2 \times 8 \times 10^{-4}}{10 \times 10^{-3}} = 0.16 \)

Now using \( V^2 = 2a_t s \Rightarrow a_t = \frac{V^2}{2s} = \frac{0.16}{2 \times 8.0384} \approx 0.1\,\text{m/s}^2 \)

Hence, the answer is option 1.

Ques 3: A ball is thrown vertically downward with a velocity of 20 m/s from the top of a tower. It hits the ground after some time with a velocity of 80 m/s. The height of the tower is: (g = 10 m/s)

Option 1: 360 m

Option 2: 340 m

Option 3: 320 m

Option 4: 300 m

Difficulty level: Medium

Answer:

Given:

Initial velocity, \( u = 20\,\text{m/s} \) (downward)

Final velocity, \( v = 80\,\text{m/s} \)

Acceleration due to gravity, \( g = 10\,\text{m/s}^2 \)

Let the height of the tower be \( h \)

Using the kinematic equation:

\( v^2 = u^2 + 2gh \)

Substitute values:

\( (80)^2 = (20)^2 + 2 \cdot 10 \cdot h \)

\( \Rightarrow 6400 = 400 + 20h \)

\( \Rightarrow 20h = 6000 \)

\( \Rightarrow h = \frac{6000}{20} = 300\,\text{m} \)

Final Answer: Option 4) \( 300\,\text{m} \)

Alternate method:

\( v^2 - u^2 = 2as \)

\( (80)^2 - (20)^2 = 2 \times 10 \times h \)

\( h = \frac{6400 - 400}{20} = \frac{6000}{20} = 300\,\text{m} \)

Hence, the answer is option 4.

Ques 4: A small block slides down on a smooth inclined plane, starting from rest at time t=0. Let Sn be the distance travelled by the block in the interval t=n-1 to t=n.

Then, the ratio \( S_n / S_{n+1} \) is:

\(\text{A: } \frac{2n - 1}{2n}\)

\(\text{B: } \frac{2n - 1}{2n + 1}\)

\(\text{C: } \frac{2n + 1}{2n - 1}\)

\(\text{D: } \frac{2n}{2n - 1}\)

Difficulty level: Medium

Answer: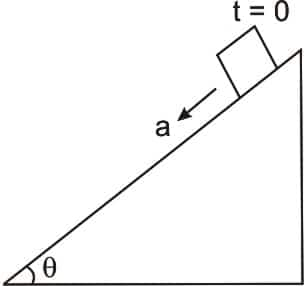

From \( t = 0 \) to \( t = n - 1 \), \( S_1 = 0 + \frac{1}{2}a(n - 1)^2 \)

From \( t = 0 \) to \( t = n \), \( S_2 = 0 + \frac{1}{2}a(n)^2 \)

From \( t = 0 \) to \( t = n + 1 \), \( S_3 = 0 + \frac{1}{2}a(n + 1)^2 \)

\( S_n = S_2 - S_1 = \frac{1}{2}a \left[ n^2 - (n^2 - 2n + 1) \right] \)

\( S_{n+1} = S_3 - S_2 = \frac{1}{2}a \left[ n^2 + 2n + 1 - n^2 \right] \)

\( \frac{S_n}{S_{n+1}} = \frac{2n - 1}{2n + 1} \)

Hence, the answer is option (2).

Ques 5: A particle moving in a circle of radius R with a uniform speed takes a time T to complete one revolution.

If this particle were projected with the same speed at an angle ′θ′ to the horizontal, the maximum height attained by it equals 4 R . The angle of projection,θ, is then given by :

Option 1: \(\theta = \cos^{-1} \left( \frac{gT^2 \pi}{2R} \right)\)

Option 2: \(\theta = \cos^{-1} \left( \frac{\pi^2 R g T^2}{2} \right)\)

Option 3: \(\theta = \sin^{-1} \left( \pi^2 R g T^2 \right)\)

Option 4: \(\theta = \sin^{-1} \left( \frac{2gT^2 \pi}{2R} \right)\)

Difficulty level: Medium

Given:

\( T = \frac{2\pi R}{V} \quad \text{and} \quad V = \frac{2\pi R}{T} \)

Range:

\( R = \frac{u^2 \sin 2\theta}{g} \Rightarrow u = 2 \sin \theta \)

Height:

\( H = \frac{V^2 \sin^2 \theta}{2g} = \frac{(2gH)(4\pi^2 R^2)}{T^2} \)

From this,

\( \sin \theta = \sqrt{ \frac{2gH T^2}{4\pi^2 R^2} } \Rightarrow \sin \theta = \frac{2gT^2 \pi}{2R} \)

Therefore,

\( \theta = \sin^{-1} \left( \frac{2gT^2 \pi}{2R} \right) \)

Ques 6: The ratio of the distances travelled by a freely falling body in the 1st, 2nd, 3rd and 4th second :

Option 1: 1: 4: 9: 16

Option 2: 1: 3: 5: 7

Option 3: 1: 1: 1: 1

Option 4: 1: 2: 3: 4

Difficulty level: Medium

Answer: The initial speed of the body is zero, i.e. u=0

Distance travelled in the \(n^\text{th}\) second is given by:

\( S_n = u + \frac{a}{2}(2n - 1) \)

\(\Rightarrow S_n = \frac{a}{2}(2n - 1) \quad (\text{since } u = 0)\)

So, distance travelled in the 1st second:

\( S_1 = \frac{a}{2}(2 \times 1 - 1) = \frac{a}{2} \)

So, distance travelled in the 2nd second:

\( S_2 = \frac{a}{2}(2 \times 2 - 1) = \frac{3a}{2} \)

So, distance travelled in the 3rd second:

\( S_3 = \frac{a}{2}(2 \times 3 - 1) = \frac{5a}{2} \)

So, distance travelled in the 4th second:

\( S_4 = \frac{a}{2}(2 \times 4 - 1) = \frac{7a}{2} \)

\(\Rightarrow S_1 : S_2 : S_3 : S_4 = 1 : 3 : 5 : 7\)

By Galileo's ratio, the distance travelled by a freely falling body is in the ratio \(1 : 3 : 5 : 7\) (odd numbers).

Hence, the answer is option (2).

Ques 7: A ball is projected with a velocity 10 ms−1 at an angle of 60∘ with the vertical direction. Its speed at the highest point of its trajectory will be:

Option 1: 53 ms−1

Option 2: 5 ms−1

Option 3: 10 ms−1

Option 4: Zero

Difficulty level: Medium

Answer:

At the topmost position, the speed of the projectile is \( u \cos \theta = 10 \cos 30^\circ = 5\sqrt{3} \, \text{m/s} \).

Hence, the answer is option 1.

Kinematics Concept Summary: Key Formulas & Exam Tips

Important Formulas

Here are some important formulas which serve as a base for Kinematics:

• Equations of Motion: \( v = u + at \), \( s = ut + \frac{1}{2}at^2 \), \( v^2 = u^2 + 2as \), \( v = u + at \)

• Projectile Motion:

  Time of flight: \( T = \frac{2u \sin \theta}{g} \)

  Maximum height: \( H = \frac{u^2 \sin^2 \theta}{2g} \)

  Range: \( R = \frac{u^2 \sin 2\theta}{g} \)

Graphical Analysis:

• The slope of a position-time graph gives velocity.

• The slope of a velocity-time graph is acceleration.

• Relative Velocity

Final Tips for Mastering Kinematics in NEET

• Understand motion graphs deeply, as they appear frequently in PYQs.

• Master vectors because this helps in relative motion & projectile problems.

• Avoid calculation errors & unit conversion mistakes as these cost valuable marks.

• Practice PYQs & NEET mock tests as they help build accuracy & confidence.

Thus, with consistent practice and conceptual clarity, Kinematics can become one of your strongest topics in NEET Physics. Keep solving PYQs, focus on tricky concepts, and revise formulas regularly. Practice, Practice, Practice!