Careers360 Logo
Medicine and Allied Sciences
Search Colleges, Exams, Schools & more
Know About NEET First Order Reaction Topic, Questions And Solutions

Know About NEET First Order Reaction Topic, Questions And Solutions

Edited By Sumit Saini | Updated on Jun 06, 2022 12:13 PM IST | #NEET
Upcoming Event
NEET  Admit Card Date : 01 May' 2025 - 01 May' 2025

First Order Reaction

Chemical Kinetics is one of the important chapters of class 12 Chemistry. It generally deals with understanding the rate of chemical reactions. Rate of chemical reaction is the speed at which chemical reaction takes place. Reaction rate is influenced by many factors including temperature, pressure, catalyst etc.

Know About NEET First Order Reaction Topic, Questions And Solutions
Know About NEET First Order Reaction Topic, Questions And Solutions

Reactions are classified in various orders like zero order reaction, First order reaction, second order reaction among others on the basis of rate law followed by them.

A first-order reaction refers to the reaction in which the rate of reaction is proportional to the first power of concentration of the reactant at any point of time. Hence, higher the concentration of reactant, higher will be the rate of reaction. Rate of first order reaction decreases as it proceeds due to decrease in concentration of reactant.

Background wave

Hence in first order reaction, rate of reaction is directly proportional to the concentration of reactant as described in the equation below.

Reaction-

Reactant →Product

Rate =k[Reactant]

Below are some of the examples of First Order reaction

2N2O5 → 4NO2+O2

Rate = k[N2O5]

2H2O2 → 2H2O + O2

Rate = k[H2O2]

After analysing the last five years of NEET papers, it has been observed that, total 10 questions were asked from the Chemical Kinetics Chapter and out of those, four questions belong to First order reaction. This shows that First order reaction is the most important concept of Chemical Kinetics and most of the questions can be solved if Integral form of first order reaction is understood well. Questions asked from first order reactions are discussed in the article below.

Differential Rate Law for First Order reaction

Differential Rate Law for a First-Order Reaction reflects the change in concentration with respect to time which is shown by equation below:

Let us assume a first order reaction: A(Reactant)→B(Product)

Rate = -d[A]/dt = k[A]1 = k[A]

In the above equation,

  • ‘k’ represents the rate constant of the first-order reaction, the unit of the rate constant is s-1.

  • ‘[A]’ represents the concentration of the reactant.

  • d[A]/dt represents the change in the concentration of reactant ‘A’ with respect to time.

Integrated Rate Law for First-Order Reaction

Integrated Rate Law of first order reaction is used to calculate the value of rate of rate constant, concentration of reactant a given time, half life etc. Most of the numericals are solved by using Integrated rate law only. Differential rate law is used to obtain the Integral rate law of a First order reaction.

Differential rate law is: -d[A]/dt = k[A]

\Rightarrow d[A]/dt = -k[A]

Integrating both sides, we get

\begin{array}{l}\int_{[A]_0}^{[A]}\frac{d[A]}{[A]} = -\int_{t_0}^{t}kdt\end{array}

Where [A]o is concentration of reactant at time t0 s, and [A] is the concentration of reactant at time t. We get,

\Rightarrow \begin{array}{l}\int_{[A]_0}^{[A]}\frac{1}{[A]}d[A] = -\int_{t_0}^{t}kdt\end{array}

Considering t0 =0, and solving the equation, we get

\Rightarrow ln[A] – ln[A]0 = -kt

\Rightarrow ln[A] =ln[A]0 -kt

Raising each side to component e, we get

\Rightarrow \begin{array}{l}e^{ln[A]} = e^{(ln[A]_0-kt)} \end{array}

\Rightarrow \begin{array}{l}[A] = [A]_0 e^{-kt}\end{array}

Hence, \begin{array}{l}[A] = [A]_0 e^{-kt}\end{array} is the final expression in the integrated form for first order reaction. The above derivation is useful in solving many numerical problems.

Using the Integrated Rate law, Concentration v/s time Graph for First order reaction can be obtained which is shown below

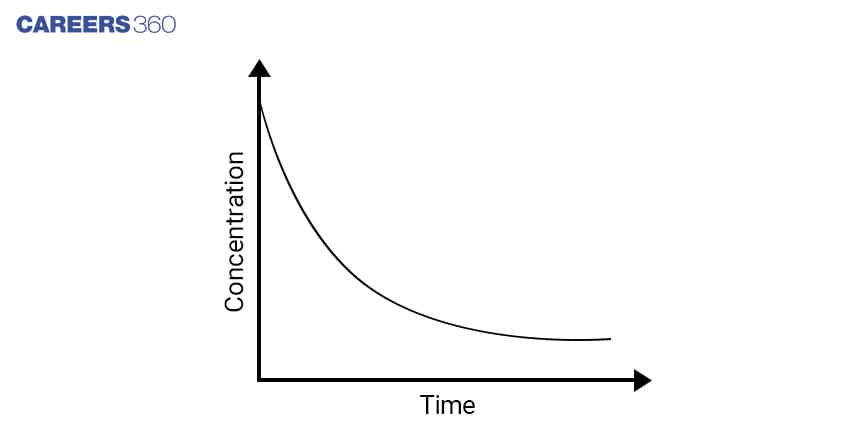
Concentration-time


As the first-order reaction follows the equation ln[A] = ln[A]0 – kt which is similar to that of a straight line (y = mx + c) with slope -k. Hence, this equation can be plotted as-

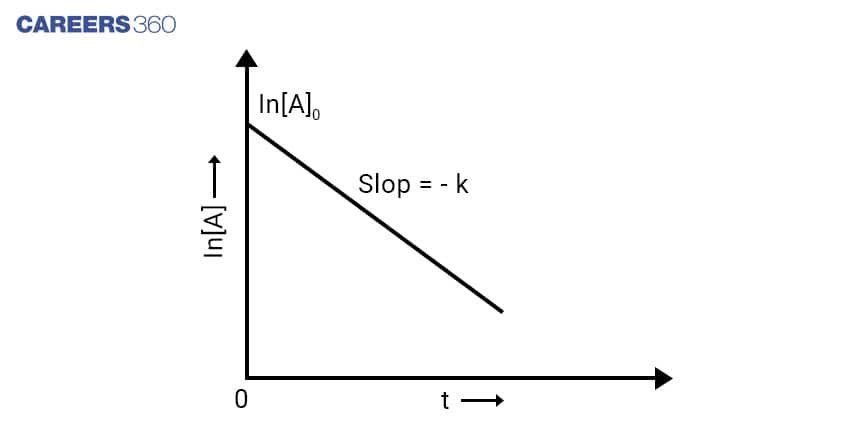
1653634323010

From the above graph, it can be said that the graph for ln[A] v/s t for a first-order reaction is a straight line with slope -k.

Half-Life of a First-Order Reaction

The half-life of a chemical reaction refers to the time required by the reactant concentration to become half of its initial value. It is represented by t_\frac{1}{2}.

Hence, according to the first order reaction, \begin{array}{l}[A] = [A]_0 e^{-kt}\end{array}. Where [A] refers to the concentration of the reactant at any time ‘‘t’’ and [A]o represents the initial concentration of the reactant.

At half life, t = t1/2 , [A] =A0/2

Putting the value of [A] =A0/2 and t = t1/2 in the equation \begin{array}{l}[A] = [A]_0 e^{-kt}\end{array}, we get

\begin{array}{l}\frac{[A]_0}{2} = [A]_0 e^{-kt_{1/2}}\end{array}

\begin{array}{l}e^{-kt_{1/2}}\end{array}=\frac{1}{2}

Taking ln on both sides, we get,

\begin{array}{l}ln(\frac{1}{2}) = -kt_{1/2}\end{array}

\begin{array}{l}\ t_{1/2} = \frac{0.693}{k}\end{array}

Hence half life of the first order reaction is 0.693/k, where k is the rate constant.

Below discussed are some of the questions asked in the NEET exam from first order reaction.

Question 1. A first order reaction has a specific reaction rate of 10-2 sec-1. How much time will it take for 20 g of the reactant to reduce to 5 g? [NEET 2017]

  1. 238.6 sec

  2. 138.6 sec

  3. 346.5 sec

  4. 693.0 sec

Most Scoring concepts for NEET
This ebook serves as a valuable study guide for NEET exams, specifically designed to assist students in light of recent changes and the removal of certain topics from the NEET exam.
Download EBook

Ans. The rate of first order reaction is proportional to the first power of the concentration of the reaction.

Let us consider a reaction, R → P , wherein

R → P

At t=0 a 0

At t=t a-x x

rate[r]=K[R]^{1}

\frac{-d(a-x)}{dt}=K(a-x)

After solving this equation, we get

t= \frac{2.303}{k} log \frac{a}{a-x}

Now, putting the values

t= \frac{2.303}{10^{-2}} log \frac{20}{5}

t= 138.6 sec

Alternatively, this can be solved by the half life method. According to which after the first half life concentration becomes half and after the second half life, concentration becomes ¼ th of the initial concentration. Hence after two half life, the concentration becomes from 20g to 5g.

t_\frac{1}{2}=\frac{0.693}{k}

t_\frac{1}{2} \:\:of \:\:the \:\:reaction=\frac{0.693}{K}

\frac{0.693}{10^{-2}}sec=69.3\:sec

Now, 2t1/2= 69.3×2= 138.6 sec.

Hence option ‘’C’’ is correct.

Question 2. The correct difference between first and second-order reactions is that [NEET 2018]

  1. a first-order reaction can be catalysed; a second-order reaction cannot be catalysed

  2. the half-life of a first-order reaction does not depend on [A]o; the half-life of a second-order reaction does depend on [A]o

  3. the rate of a first-order reaction does not depend on reactant concentrations; the rate of a second-order reaction does depend on reactant concentrations

  4. the rate of a first-order reaction does depend on reactant concentrations; the rate of a second-order reaction does not depend on reactant concentrations

Ans. For first Order reaction, rate is directly proportional to the first power of concentration.

For a reaction, A→B

Rate = -d[A]/dt = k[A] and half life is

t_\frac{1}{2}=\frac{0.693}{k}

Where unit of k=sec^{-1}.

Hence \left ( t_{\frac{1}{2}} \right ) 1^{st} order = Independent \; of \; concentration

For second order reaction, For a reaction, A→B

Rate = k[A]^2 and its half life is t_{1/2}= \frac{1}{k[A]_o}

\left ( t_{\frac{1}{2}} \right ) 2^{nd} order \alpha \frac{1}{Initial \;Concentration}

Hence, The half-life of a first-order reaction does not depend on [A]o; the half-life of a second-order reaction does depend on [A]o

Option B is correct.

Question 3. If the rate constant for a first order reaction is k, the time (t) required for the completion of 99 per cent of the reaction is given by: [NEET 2019]

  1. t = 0.693/k

  2. t = 6.909/k

  3. t = 4.606/k

  4. t = 2.303/k

Ans. Let us consider a reaction, R → P , wherein

R → P

At t=0 a 0

At t=t a-x x

For the First Order reaction, Rate of reaction is proportional to the first power of the concentration of the reaction.

rate[r]=K[R]^{1}

\frac{-d(a-x)}{dt}=K(a-x)

ln \:[\frac{a}{a-x}]=kt \:(Integrated rate law)

Unit of k=sec^{-1}

t_\frac{1}{2}=\frac{0.693}{k} and

t= \frac{2.303}{k}\log_{10}\frac{a}{a-x}

a = 100\%\;\;\;\;x=99\%

a - x= 1\%

t_{99.9%} = \frac{2.303}{k}\log_{10}\frac{100}{1} = \frac{2.303}{k}\log_{10}10^2

t_{99.9%} = \frac{2.303}{k}\times 2 = \frac{4.606}{k}

Hence option C is correct.

Question 4. The rate constant for a first order reaction is 4.606 \times 10^{-3}s^{-1} The time required to reduce 2 g of the reactant to 0.2g is: [NEET 2020]

  1. 1000s

  2. 100s

  3. 200s

  4. 500s

Ans. Given,

K=4.606 \times 10^{-3}s^{-1}

Hence the given reaction is of first order.

Thus, we have:

\mathrm{K\: t\: =\: ln\frac{A_{o}}{A}}

Hence it is from the option of keeping th

\mathrm{4.606\: x\: 10^{-3}\: t\: =\: 2.303log\left (\frac{2}{0.2} \right )}

Thus, t=0.5\times10^{3}\; \text {sec}

\text {t}=500\; \text {sec}

Therefore, Option(D) is correct.

Articles

Upcoming Medicine Exams

Common Nursing Entrance Test

Application Date:24 March,2025 - 26 April,2025

KGMU BSc Nursing Exam

Application Correction Date:19 April,2025 - 26 April,2025

National Eligibility cum Entrance Test

Choice of Exam City:26 April,2025 - 26 April,2025

Amrita Entrance Examination – Life Sciences, Agriculture & Medical Sciences

Exam Date:12 May,2025 - 12 May,2025

Joint Entrance Test for Nursing, Paramedical and Allied Sciences Under Graduate Courses

Exam Date:25 May,2025 - 25 May,2025

View All Medicine Exams

Certifications By Top Providers

Forensic Science DNA Analysis
 Via University of Cambridge, Cambridge
Introduction to Psychology
 Via San Jose State University, San Jose
AMC Clinical Exam Preparation
 Via Academically
OPRA Exam Preparation
 Via Academically
Become a Pharmacy Preceptor
 Via Taipei Medical University, Taipei
Radiology Technician
 Via VIVO Healthcare
Coursera
 355 courses
Futurelearn
 310 courses
Edx
 233 courses
Udemy
 191 courses
Swayam
 106 courses
Johns Hopkins University, Baltimore
 75 courses

Explore Top Universities Across Globe

University College London, London
  Gower Street, London, WC1E 6BT
University of Essex, Colchester
  Wivenhoe Park Colchester CO4 3SQ
University of Nottingham, Nottingham
  University Park, Nottingham NG7 2RD
University of Alberta, Edmonton
  116 St. and 85 Ave., Edmonton, Alberta, Canada T6G 2R3
University of Liverpool, Liverpool
  Liverpool L69 3BX
University of Wisconsin, Madison
  329 Union South 1308 W. Dayton Street Madison, WI 53715-1149

Popular Courses and Specializations

Popular Degrees

Popular Branches

List of colleges accepting NEET

Browse Medicine Colleges by State

Related E-books & Sample Papers

Questions related to NEET

Have a question related to NEET ?
How to get admission in bams college without neet

Hello dear,

To get admission to a BAMS course without NEET, here are a few possible routes:

  1. State-Level Exams: Some states, like Karnataka, Maharashtra, or Uttarakhand, may conduct their own entrance exams for BAMS admissions. These may not require NEET scores.

  2. Private Colleges & Management/NRI Quota: Some private colleges may offer admission through management or NRI quotas without requiring NEET scores, although the fees may be higher.

  3. Special Exemptions: Rarely, some colleges may offer exemptions or internal entrance exams, but this is not common.

Make sure the college is recognized by (CCIM) to ensure the degree is valid. Always verify the latest admission guidelines from the specific state or college.

Read Complete Answer
Devanshi Goyal 01 April,2025
In the month may 2025, I will get my 12 result .. So I want government college for bsc in microbiology.so suggest some ..I had not given neet and cuet ..so without that suggest me ..

Dear

If you're looking to pursue a BSc in Microbiology from a government college without appearing for NEET or CUET, you can still explore many excellent options. Most government colleges admit students to BSc courses based on the marks obtained in your 12th-grade exams. Here are some of the top government colleges you can consider for BSc in Microbiology:

1. University of Delhi (DU)

  • Courses: DU offers a BSc (Hons) in Microbiology.
  • Admission Process: Based on 12th-grade marks and cutoffs, which vary every year.
  • Eligibility: You need to have Biology as a subject in Class 12 and meet the cutoff requirements.

2. Banaras Hindu University (BHU)

  • Courses: BHU offers a BSc in Microbiology.
  • Admission Process: Admission is usually based on the entrance test, but if you’re looking for colleges with direct 12th marks-based admission, consider other options.
  • Eligibility: A science background with Biology in Class 12 is required.

3. University of Calcutta

  • Courses: BSc in Microbiology.
  • Admission Process: Based on merit (your 12th-grade marks).
  • Eligibility: Completion of Class 12 with Biology as one of the subjects.

4. Jamia Millia Islamia (JMI)

  • Courses: BSc in Microbiology.
  • Admission Process: Based on 12th marks or an entrance exam, depending on the course.
  • Eligibility: Biology should be one of the subjects in Class 12.

5. Madras University

  • Courses: BSc in Microbiology.
  • Admission Process: Based on merit, considering your marks in 12th.
  • Eligibility: A science background in Class 12 with Biology.

6. University of Pune (Savitribai Phule Pune University)

  • Courses: BSc in Microbiology.
  • Admission Process: Based on 12th-grade marks.
  • Eligibility: Biology as a subject in Class 12.

7. Karnataka University, Dharwad

  • Courses: BSc in Microbiology.
  • Admission Process: Based on marks obtained in the Class 12 exam.
  • Eligibility: Class 12 with a science background and Biology as a subject.

8. St. Xavier’s College, Mumbai

  • Courses: BSc in Microbiology.
  • Admission Process: Based on Class 12 marks.
  • Eligibility: Science stream with Biology in 12th.

9. Aligarh Muslim University (AMU)

  • Courses: BSc in Microbiology.
  • Admission Process: Based on entrance tests or merit, depending on the course.
  • Eligibility: Completion of Class 12 with Biology.

10. Sri Venkateswara College, Delhi University

  • Courses: BSc (Hons) Microbiology.
  • Admission Process: Based on Class 12 marks through the DU admission process.
  • Eligibility: Class 12 with Biology as a subject.

Tips:

  • Research and Apply Early: Keep an eye on the official websites for admission dates and specific criteria.
  • Check Cutoffs: Colleges like DU and BHU release cutoff lists, which are based on your 12th-grade performance. Ensure you meet the required percentage.
  • Prepare Documents: Make sure to have your Class 12 marksheet and necessary documents ready for the application.

These colleges offer great opportunities for pursuing BSc in Microbiology, and you do not need to appear for NEET or CUET for admission to these programs.

Read Complete Answer
Shivanshu 31 March,2025
what is cutoff for general student in neet 2025

Here’s the cutoff information of neet 2025 for general students:-

  • NEET 2025 cut-off : Official cut-off marks for General students will be released after the NEET 2025 results.

  • Expected range : The anticipated cut-off for General (UR/EWS) students is likely to fall between 720-162 marks, based on previous trends.

  • Percentile requirement : A minimum of 50th percentile is required for General category candidates to qualify.

  • Factors influencing the cut-off :

    • Difficulty level of the exam

    • Number of candidates appearing

    • Seat availability across medical colleges

  • Final announcement : The official cut-off will be published by NTA after the NEET results are processed.

Read Complete Answer
Devanshi Goyal 31 March,2025
Is samay neet ka phise kitna chal raha hai

The NEET 2025 application fees were as follows:


General Category: Rs1,700


General-EWS/OBC-NCL: Rs1,600

SC/ST/PwBD/Third Gender: Rs1,000

Candidates appearing from outside India were required to pay a higher fee of Rs9,500.

The application fee was payable online through various modes, including debit card, credit card, net banking, UPI, or e-wallet.

Read Complete Answer
Devanshi Goyal 31 March,2025
Is samay neet ka phise kitna chal raha hai

Hello,

As of March 2025, the NEET application fees are:

- General Category:1,700

- General-EWS/OBC-NCL:1,600

- SC/ST/PwD/Third Gender:1,000

- NRI Candidates:9,50

Fees are payable online via net banking, credit/debit cards, or UPI.

hope this helps you,

Thank you

Read Complete Answer
Tanya Gupta 30 March,2025
View All

Popular NEET Questions

Column I ( Salivary gland)

 

Column II ( Their location)

Parotids

I

Below tongue

Sub-maxillary / sub-mandibular

Ii

Lower jaw

Sub-linguals

Iii

Cheek
Option: 1

a(i), b(ii) , c(iii)

 


Option: 2

a(ii), b(i), c(iii)

 


Option: 3

a(i), b(iii), c(ii)


Option: 4

a(iii), b(ii), c(i)


Read More

Ethyl \; ester \xrightarrow[(excess)]{CH_{3}MgBr} P

the product 'P' will be ,

Option: 1


Option: 2


Option: 3

\left ( C_{2}H_{5} \right )_{3} - C- OH


Option: 4


Read More

 

    

           

 Valve name                            

              

Function
    I   Aortic valve     A

Prevents blood from going backward from the pulmonary artery to the right ventricle.
    II   Mitral valve     B

 Prevent blood from flowing backward from the right ventricle to the right atrium.
    III   Pulmonic valve     C

 Prevents backward flow from the aorta into the left ventricle.
    IV   Tricuspid valve     D

 Prevent backward flow from the left ventricle to the left atrium.

 

Option: 1

I – A , II – B, III – C, IV – D


Option: 2

 I – B , II – C , III – A , IV – D


Option: 3

 I – C , II – D , III – A , IV – B


Option: 4

 I – D , II – A , III – B , IV – C 

 

 


Read More

Column A Column B
A

a) Organisation of cellular contents and further cell growth.  
B

b) Leads to formation of two daughter cells.
C

c) Cell grows physically and increase volume proteins,organells.
D

d)  synthesis and replication of DNA.

Match the correct option as per the process shown in the diagram. 

 

 

 

Option: 1

1-b,2-a,3-d,4-c
 


Option: 2

1-c,2-b,3-a,4-d


Option: 3

1-a,2-d,3-c,4-b

 


Option: 4

1-c,2-d,3-a,4-b


Read More

0.014 Kg of N2 gas at 27 0C is kept in a closed vessel. How much heat is required to double the rms speed of the N2 molecules?

Option: 1

3000 cal


Option: 2

2250 cal


Option: 3

2500 cal


Option: 4

3500 cal


Read More

0.16 g of dibasic acid required 25 ml of decinormal NaOH solution for complete neutralisation. The modecular weight of the acid will be

Option: 1

32


Option: 2

64


Option: 3

128


Option: 4

256


Read More

0.5 F of electricity is passed through 500 mL of copper sulphate solution. The amount of copper (in g) which can be deposited will be:

Option: 1

31.75


Option: 2

15.8


Option: 3

47.4


Option: 4

63.5


Read More

0.5 g of an organic substance was kjeldahlised and the ammonia released was neutralised by 100 ml 0.1 M HCl. Percentage of nitrogen in the compound is

Option: 1

14


Option: 2

42


Option: 3

28


Option: 4

72


Read More

0xone is

Option: 1

\mathrm{KO}_{2}


Option: 2

\mathrm{Na}_{2} \mathrm{O}_{2}


Option: 3

\mathrm{Li}_{2} \mathrm{O}


Option: 4

\mathrm{CaO}


Read More

(1) A substance  known as "Smack"

(2) Diacetylmorphine

(3) Possessing a white color

(4) Devoid of any odor

(5) Crystal compound with a bitter taste

(6) Obtained by extracting from the latex of the poppy plant

The above statements/information are correct for:

Option: 1

Morphine


Option: 2

Heroin


Option: 3

Cocaine


Option: 4

Barbiturates


Read More

Explore Career Options (By Industry)

Orthotist and Prosthetist

Orthotists and Prosthetists are professionals who provide aid to patients with disabilities. They fix them to artificial limbs (prosthetics) and help them to regain stability. There are times when people lose their limbs in an accident. In some other occasions, they are born without a limb or orthopaedic impairment. Orthotists and prosthetists play a crucial role in their lives with fixing them to assistive devices and provide mobility.

6 Jobs Available
Pathologist

A career in pathology in India is filled with several responsibilities as it is a medical branch and affects human lives. The demand for pathologists has been increasing over the past few years as people are getting more aware of different diseases. Not only that, but an increase in population and lifestyle changes have also contributed to the increase in a pathologist’s demand. The pathology careers provide an extremely huge number of opportunities and if you want to be a part of the medical field you can consider being a pathologist. If you want to know more about a career in pathology in India then continue reading this article.

5 Jobs Available
Veterinary Doctor

A veterinary doctor is a professional, working in animal healthcare. He or she conducts medical examinations, diagnoses, and treats various illnesses of animals. Animals have distinct internal organs and functions, requiring specialised attention from a veterinary doctor. A doctor who treats humans cannot offer the same level of care to animals due to these variations. Therefore, a veterinary doctor plays a critical role in animal welfare.

Veterinary professionals prevent illness by providing vaccines and offering advice on animal nutrition and overall health. Their knowledge extends beyond household animals and includes livestock, wildlife, and exotic animals. Individuals who love animals and want to treat their illnesses, injuries, and diseases must opt for a career as a veterinary doctor.

5 Jobs Available
Speech Therapist

Speech therapists are essential medical professionals addressing speech disorders. Whether it's delayed speech in children or difficulties in pronunciation, these experts play a crucial role. This article explores how to become a speech therapist in India, covering courses, colleges, and the responsibilities of this impactful profession.

4 Jobs Available
Gynaecologist

Gynaecology can be defined as the study of the female body. The job outlook for gynaecology is excellent since there is evergreen demand for one because of their responsibility of dealing with not only women’s health but also fertility and pregnancy issues. Although most women prefer to have a women obstetrician gynaecologist as their doctor, men also explore a career as a gynaecologist and there are ample amounts of male doctors in the field who are gynaecologists and aid women during delivery and childbirth. 

4 Jobs Available
Audiologist

The audiologist career involves audiology professionals who are responsible to treat hearing loss and proactively preventing the relevant damage. Individuals who opt for a career as an audiologist use various testing strategies with the aim to determine if someone has a normal sensitivity to sounds or not. After the identification of hearing loss, a hearing doctor is required to determine which sections of the hearing are affected, to what extent they are affected, and where the wound causing the hearing loss is found. As soon as the hearing loss is identified, the patients are provided with recommendations for interventions and rehabilitation such as hearing aids, cochlear implants, and appropriate medical referrals. While audiology is a branch of science that studies and researches hearing, balance, and related disorders.

3 Jobs Available
Oncologist

An oncologist is a specialised doctor responsible for providing medical care to patients diagnosed with cancer. He or she uses several therapies to control the cancer and its effect on the human body such as chemotherapy, immunotherapy, radiation therapy and biopsy. An oncologist designs a treatment plan based on a pathology report after diagnosing the type of cancer and where it is spreading inside the body.

3 Jobs Available
Anatomist

Are you searching for an ‘Anatomist job description’? An Anatomist is a research professional who applies the laws of biological science to determine the ability of bodies of various living organisms including animals and humans to regenerate the damaged or destroyed organs. If you want to know what does an anatomist do, then read the entire article, where we will answer all your questions.

2 Jobs Available
Narcotics Officer

A Narcotics Officer is an officer employed by the state to investigate the usage of drugs and their trafficking. A narcotics officer conducts undercover operations, investigates suspected drug dealers, executes raids and other appropriate actions for arresting these traffickers to reduce the circulation of drugs in the country. 

A narcotics officer works in collaboration with other government agencies to stop drug trafficking at borders. He or she engages with various NGOs and public organisations to teach people about the dangerous effects of drug usage. A narcotics officer plays an important role in reducing the illegal activities of drug dealers and the circulation of drugs in the nation.

4 Jobs Available
Research Associate

If we talk about a career as a research associate, it all comes down to one thing - curiosity towards nature and the passion to find answers. A career as a research associate is full of thrill and excitement. However, a research associate also faces a lot of challenges and failures while working on a project. A job of a research associate includes a spectrum of Science as a subject in detail. 

2 Jobs Available
Drug Inspector

A career as a Drug Inspector is regarded as one of the most diverse in the field of healthcare and pharmacy. Candidates must undergo a screening process administered by the UPSC and or SPSCs in order to become drug inspectors. Those who manage it through the selection process will have a rewarding career with a high salary.

2 Jobs Available
Biotechnologist

A Biotechnologist is a professional who possesses strong knowledge and techniques that are utilised in creating and developing innovative products that improve the quality of human life standards. A biochemist uses biological organisms to create and improve goods and procedures for agriculture, medicine, and sustainability. He or she researches the genetic, chemical, and physical characteristics of cells, tissues, and organisms to determine how they can be used industrially.

2 Jobs Available
R&D Personnel

A career as R&D Personnel requires researching, planning, and implementing new programs and protocols into their organization and overseeing new products’ development. He or she uses his or her creative abilities to improve the existing products as per the requirements of the target market.

2 Jobs Available

Study Resources, Applications and Opportunities

MAHE Manipal B.Sc Nursing 2025
MAHE Manipal B.Sc Nursing 2025
Apply

Accorded Institution of Eminence by MoE, Govt. of India | NAAC A++ Grade | Ranked #4 India by NIRF 2024

MAHE Manipal Allied Health Sciences 2025
MAHE Manipal Allied Health Sciences 2025
Apply

Accorded Institution of Eminence by MoE, Govt. of India | NAAC A++ Grade | Ranked #4 India by NIRF 2024

NEET College Predictor
NEET College Predictor
Start

Know possible Govt/Private MBBS/BDS Colleges based on your NEET rank

NEET Companion
Apply

Register for Careers360 NEET Counseling & Admission Guidance Service.

VIT Bhopal University | Integrated M.Sc Biotechnology 2025
Apply

Apply for Integrated M.Sc Biotechnology (5 Years, after 10+2) @ VIT Bhopal University | H-CTC 52 LPA

TOEFL ® Registrations 2024
Apply

Accepted by more than 11,000 universities in over 150 countries worldwide

View All Application Forms
News and Notifications
NEET MBBS cut-off rises for Bangalore Medical College, drops for other Karnataka govt colleges
April 02, 2025 - 04:59 PM IST
Aiming for 650+ in NEET 2025? Focus on these high-weightage chapters
April 01, 2025 - 11:55 AM IST
Sri Chaitanya Academy, Infinity Learn launch NEET preparation course, 'ATREYA'
March 29, 2025 - 10:13 PM IST
Lowest NEET cut-off for MBBS in Maharashtra government medical colleges; passing mark out of 720
March 26, 2025 - 09:34 AM IST
NEET aspirant from Bihar dies by suicide in Kota hostel; ninth incident this year
March 26, 2025 - 07:17 AM IST
Medical courses after Class 12th without NEET 2025; course-wise eligibility, career prospectus
March 21, 2025 - 08:38 PM IST
Aakash launches free rapid revision course for NEET; paid crash course for JEE Advanced
March 21, 2025 - 03:32 PM IST

Stay up-to date with NEET News

Back to top