Refraction Through A Prism Made Easy To Ace NEET

The unit Optics has two chapters namely. Ray Optics And Optical Instruments; and Wave Optics. The unit Optics is important for the NEET UG exam as 22 questions were asked from the unit in the last five years’ papers (2017 to 2021). Out of these 22 questions, 11 were from the chapter Ray Optics And Optical Instruments and 11 from Wave Optics. Four questions out of 11 from Ray Optics were from the concept of Refraction Through A Prism. So, Refraction Through A Prism is an important topic for NEET. At the same time, JEE Main Papers also has a number of questions from the concept of Refraction Through A Prism. So, preparing this topic, that is, Refraction Through A Prism, is important for you to score well in both these entrance exams, NEET and JEE Main.

NEET 2025: Biology: Mind Maps & Important Diagrams | Mock Test (Free)

NEET 2025: Syllabus | Most Scoring concepts | NEET PYQ's (2015-24)

New: Meet Careers360 experts in your city and get guidance on shortlisting colleges

New Programme: B.E. Environmental & Sustainability @ BITS Pilani for PCB Candidates

Refraction Through A Prism

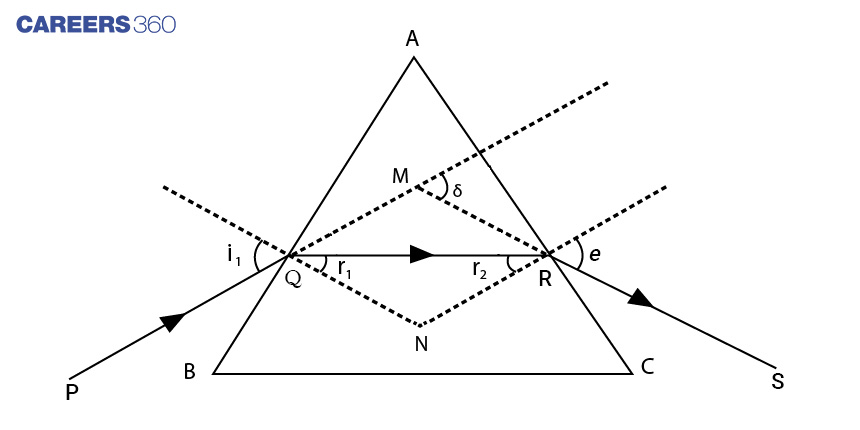
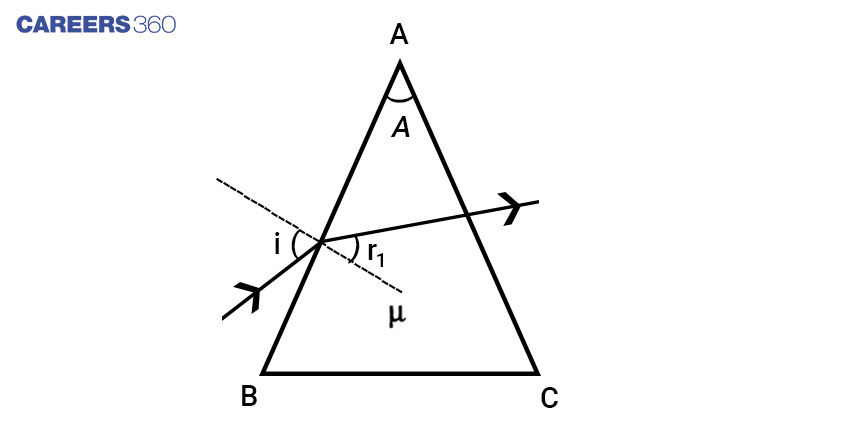
Consider a triangular prism of refractive index n. It has two triangular bases and three rectangular lateral surfaces. These surfaces are inclined to each other. The angle between its two lateral faces is called the angle of the prism A . is the angle included between the two refracting faces of the prism. is also known as refracting angle. i and r₁ are angles of incidence and refraction respectively at face AB. r₂ and e are angles of incidence and refraction respectively at face AC. e is also called the angle of emergence.

Consider the quadrilateral AQNR.

From triangle QNR

From (1) and (2)

Angle Of Deviation (δ)

The angle between the ray of incidence (PQ) and emergence (RS) is known as the angle of deviation.

The angle of deviation δ=sum of deviations at two refracting faces. That is

δ=(i-r₁)+(e-r₂)=i+e-A……(4)

Question JEE Main 2017

A ray of light is incident at an angle of on one face of a prism of angle . The emergent ray of light makes an angle of with incident ray. The angle made by the emergent ray with the second face of the prism will be:

Solution:

Given δ=30⁰, i=60⁰ and A=30⁰

δ=i+e-A

e=δ+A-i=30+30-60=0⁰. The angle made with the second face is=90⁰. So the answer is 90

Note-The angle e is with respect to the normal. There is a greater chance to mark the answer as zero which is wrong. Properly read the question to avoid this type of error.

Angle Of Minimum Deviation (δmin)

The deviation angle is minimum when i=e. When i=e, r₁=r₂=r. That refracted ray inside the prism is parallel to the base.

From equation (3)

A=2r or r=A/2

And from equation (4)

δ_min=2i-A

i=(A+δ_min)/2

Now apply the snell's law at face AB. If n is the refractive index of the prism. Let the prism be placed in the air(refractive index of the air taken as 1), then

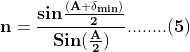
Equation (5) is the relation between the refractive index and the minimum angle of deviation of the prism.

For a thin prism, δ_min and angle A is very small. Therefore

δ_min=(n-1)A………(6)

Question: JEE Main 2019

Monochromatic light is incident at a certain angle on an equilateral triangular prism and suffers minimum deviation. If the refractive index of the material of the prism is , then the angle of incidence is:

Solution:

Since the given prism is an equilateral prism, A=60⁰

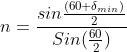
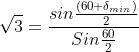
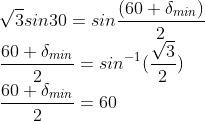
δ_min=60⁰

i=(A+δ_min)/2=(60+60)/2=60⁰. The angle of incidence is 60⁰

The Plot Of Angle Of Deviation ( δ) Versus Angle Of Incidence (i)

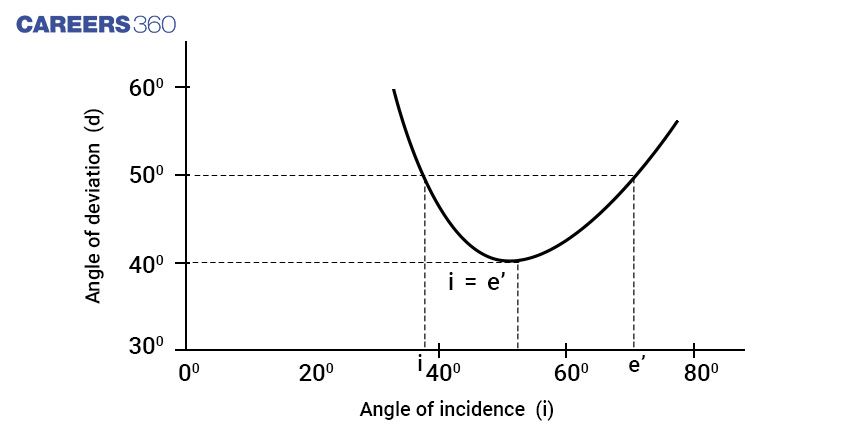
From the graph, it is clear that for deviation angles other than the minimum deviation, there are two values of i and hence for e. This implies that δ remains the same if i and e are interchanged. Let us see previous year's NEET questions based on the topic Refraction Through A Prism.

Questions From Previous 5 Year NEET Paper

Question: NEET 2017

A thin prism having refracting angle 10° is made of glass of refractive index 1.42. This prism is combined with another thin prism of glass of refractive index 1.7. This combination produces dispersion without deviation. The refracting angle of the second prism should be:

Solution:

Note: For Dispersion without deviation

Question: NEET 2018

The refractive index of the material of a prism is and the angle of the prism is 30^o. One of the two refracting surfaces of the prism is made a mirror inwards, with a silver coating. A beam of monochromatic light entering the prism from the other face will retrace its path (after reflection from the silvered surface) if its angle of incidence on the prism is

Solution:

Here r₂=0

Therefore from the relation A=r₁+r₂, r₁=A=30⁰

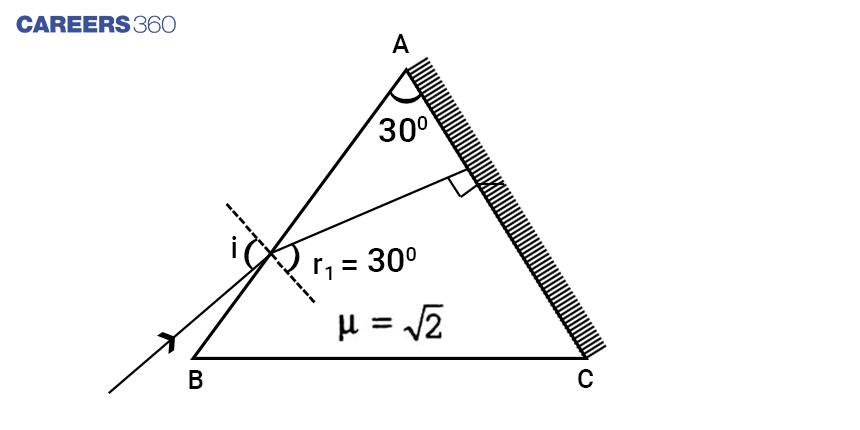
Applying snell's law at face AB

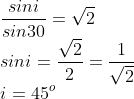
45⁰ is the angle for which the beam retraces its path.

Question: NEET 2020

A ray is incident at an angle of incidence i on one surface of a small angle prism (with the angle of prism A) and emerges normally from the opposite surface. If the refractive index of the material of the prism is then the angle of incidence is nearly equal to:

Solution:

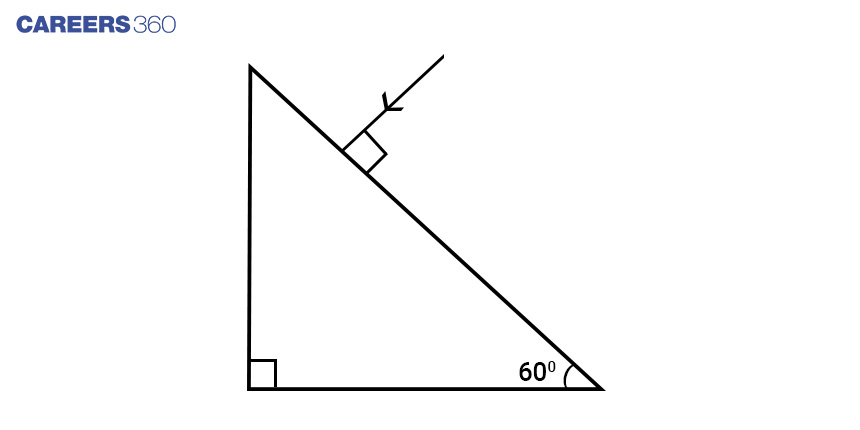
Given that ray emerges normally from the opposite surface. This implies that e=0 . Also r₂=0(angle of incidence at AC is zero, so angle of refraction at face AC is zero(e=0)). Therefore from A=r₁+r₂

A=r₁

Therefore applying snell's law for face AB

sini/sinA=

Since it is thin prism i=A

Question: NEET 2021

Find the value of the angle of emergence from the prism. The Refractive index of the glass is.

Solution:

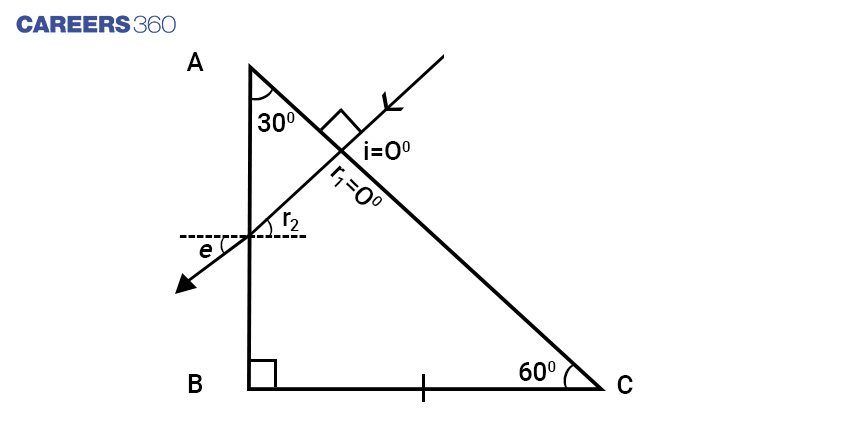
r₁=0 as i=0

Therefore A=r₂ (since A=r₁+r₂)

Applying snell's law at AB

sine/sinA=

sine=/2

e=60^o

If we look at the past five years’ papers, except 2019, all other papers have one question from the topic – Refraction Through A Prism. Eleven questions were asked from Ray Optics and out of these 4 questions were from the topic Refraction Through A Prism. That means, 36.36% of questions from Ray Optics are related to Refraction Through A Prism, which makes it an important topic. Refraction Through A Prism is a small topic and can be understood easily. To solve problems, students need to understand the Snell's Law properly and how to apply it in solving problems.