• Medicine and Allied Sciences
  • Engineering and Architecture
  • Management and Business Administration
  • Law
  • Animation and Design
  • Media, Mass Communication and Journalism
  • Finance & Accounts
  • Computer Application and IT
  • Pharmacy
  • Hospitality and Tourism
  • Competition
  • School
  • Study Abroad
  • Arts, Commerce & Sciences
  • Learn
  • Online Courses and Certifications
NEET Physics: Dual Nature Of Matter And Radiation Important Questions, Solutions

NEET Physics: Dual Nature Of Matter And Radiation Important Questions, Solutions

#NEET
Updated on 23 Jun 2022, 09:09 AM IST

If you want to become a doctor, it is important that you get a good rank in the National Eligibility cum Entrance Test (NEET) for undergraduate (UG) admissions to medical courses. And for this, you need to master all the subjects (Physics, Chemistry and Biology) included in the NEET UG syllabus. A good grip on Physics is crucial as 25% of the questions in the NEET paper is from the subject. So, how well you prepare for Physics is crucial in deciding your rank in the NEET exam, which is conducted annually.

NEET Physics: Dual Nature Of Matter And Radiation Important Questions, Solutions
Dual Nature Of Radiation And Matter Past FIve Year Papers(Image: Shutterstock)

Knowing the important topics from each chapter will be quite useful in your preparation. Here is an analysis of the previous five years' NEET questions from the Class 12 NCERT chapter, Dual Nature Of Matter And Radiation. In the Last five years of NEET paper, a total of 9 questions were asked from the Class 12 NCERT chapter, Dual Nature Of Matter And Radiation.

Topic Wise Distribution Of Questions

Topic

Number Of Questions

Einstein’s Photoelectric Equation

3

de-Broglie Wavelength

3

Concept of Electron Volt

1

Energy of Photon

1

Intensity of Light

1

The above table makes it clear that Einstein's Photoelectric Equation and the de-Broglie Wavelength are two important topics of the chapter, Dual Nature Of Matter And Radiation. Let us get a brief idea of these concepts and the NEET questions related to them.

Einstein’s Photoelectric Equation

The photoelectric equation is given by -

Kinetic Energy (K.E) of the photo-electrons = (Energy obtained from the Photon) – (The energy used to escape the metallic surface).

KE=h?-ɸ

ɸ=h?0

The energy used to escape the metallic surface is known as the work function (ɸ). Here ?0 is the threshold frequency.

Q.1 NEET - 2017

The photoelectric threshold wavelength of silver is 3250 x 10-10 m. The velocity of the electron ejected from a silver surface by the ultraviolet light of wavelength 2536 x 10-10 m is:

(Given h = 4.14 x 10-15 eVs and c = 3 x 108 ms-1)

Solution

Here the wavelengths are given.

K.E.=\frac{hc}{\lambda },\ \nu=\frac{c}{\lambda },\ \nu_0=\frac{c}{\lambda_0 }

Therefore the photoelectric equation can be written as

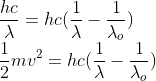
\\\frac{hc}{\lambda }=hc(\frac{1}{\lambda }-\frac{1}{\lambda _{o}})\\\frac{1}{2}mv^2=hc(\frac{1}{\lambda }-\frac{1}{\lambda _{o}})

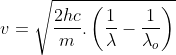
v=\sqrt{\frac{2hc}{m}.\left ( \frac{1}{\lambda }-\frac{1}{\lambda _{o}} \right )}

Given

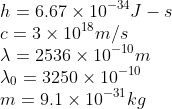
\\ h =6.67\times 10^{-34}J-s\\ c=3\times 10^{18}m/s\\ \lambda =2536\times 10^{-10}m\\ \lambda_{0} = 3250 \times 10^{-10} \\m=9.1\times 10^{-31}kg

Substituting the values the answer is

\approx 6 \times 10^5 \text{ms}^{ - 1}

Q.2 NEET - 2018

When the light of frequency 2?0 (where ?0 is threshold frequency), is incident on a metal plate, the maximum velocity of electrons emitted is ?1. When the frequency of the incident radiation is increased to 5?0, the maximum velocity of electrons emitted from the same plate is ?2. The ratio of ?1 to ?2 is

Solution

From the Einstein equation

1/2 mv^{2}= h{v}-\phi = h(v-v_{0})

Initially

1/2 mv_{1}^{2}= h(2v_{0}-v_{0})=hv_{0}

Finally

1/2 mv_{2}^{2}= h(5v_{0}-v_{0})=4hv_{0}

\Rightarrow \frac{v_{2}^{2}}{v_{1}^{2}}=4 or

\Rightarrow \frac{v_{1}}{v_{2}}=1/2

Q.3 NEET - 2021

An electromagnetic wave of wavelength λ is incident on a photosensitive surface of negligible work function. If 'm' mass is of photoelectron emitted from the surface has de-Broglie wavelength λd then:

Solution

\frac{hc}{\lambda }=\phi +kE_{max}

Momentum P = h/λd where λd is the de-Broglie wavelength, work function ɸ=0(Given)

\frac{hc}{\lambda }=0+\frac{P^{2}}{2m}=\frac{\left ( h/\lambda_d \right )^{2}}{2m}

\frac{hc}{\lambda }=\frac{h^2}{\lambda ^{2}_{d}\times 2m}

\left ( \frac{2mc}{h} \right )\lambda ^{2}_{d}=\lambda

NEET

NEET AYUSH All India Counseling

Maharashtra MBBS/BDS Counselling

Arunachal Pradesh MBBS/BDS Admissions

NEET UG

Karnataka MBBS/BDS Counselling

UP MBBS/BDS Counselling

Gujarat MBBS/BDS Counselling

Madhya Pradesh MBBS/BDS Counselling

Kerala MBBS/BDS Counselling

Tamil Nadu MBBS/BDS Counselling

Telangana MBBS/BDS Counselling

Andhra Pradesh MBBS/BDS Counselling

West Bengal MBBS/BDS Counselling

Rajasthan MBBS/BDS Counselling

Bihar MBBS/BDS

Haryana MBBS/BDS

Punjab MBBS/BDS Counselling

Chhattisgarh MBBS/BDS

Odisha MBBS/BDS

Assam MBBS/BDS

Himachal Pradesh MBBS/BDS

Jharkhand MBBS/ BDS

Jammu and Kashmir MBBS/BDS

Tripura MBBS/BDS

Puducherry MBBS/BDS

Uttarakhand MBBS/BDS

Delhi MBBS/BDS

Chandigarh MBBS/BDS Admissions

The de Broglie Wavelength Of Electron

The de-Broglie wavelength of electron λe is given by

\lambda_e = \frac{h}{m_ev}= \frac{h}{\sqrt{2m_eK}}=\frac{h}{\sqrt{2m_e(eV)}}

h=6.626\times 10^{-34} \ Js

m_e=9.1\times 10^{-31} \ kg

e=1.6\times 10^{-19} \ C

\lambda _{e }= \frac{12.27}{\sqrt{V}}A^{\circ}

The de Broglie Wavelength Associated With Charged Particle

\lambda = \frac{h}{\sqrt{2mK}}= \frac{h}{\sqrt{2mqV}}

Where K is the Kinetic Energy, m is the mass of the particle, q is the charge of the particle and V is the potential difference.

Recommended Video-

Q.4 NEET - 2017

The de-Broglie wavelength of a neutron in thermal equilibrium with heavy water at a temperature T (Kelvin) and mass m, is

Solution

Kinetic energy of the neutron in thermal equilibrium with heavy water is-

K.E=\frac{3}{2}kT

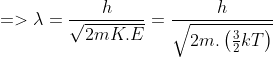
=>\lambda =\frac{h}{\sqrt{2mK.E}}=\frac{h}{\sqrt{2m.\left ( \frac{3}{2}kT \right )}}

Here K.E is the Kinetic Energy

\Rightarrow \lambda =\frac{h}{\sqrt{3mkT}}

Q.5 NEET - 2018

An electron of mass m with an initial velocity

\overset{\rightarrow}V = V_{o} \hat{i} \left ( V_{o} > 0 \right )

enters an electric field

\overset{\rightarrow}E = -E_{o} \hat{i} \left ( E_{o} = constant > 0 \right )

at t = 0 . If \lambda _{o} is its de-Broglie wavelength initially, then its de-Broglie wavelength at time t is

Options

  1. \lambda_{o}t

  2. \lambda _{o}\left ( 1 + \frac{eE_{o}}{mv_{o}}t \right )

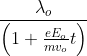
  3. \frac{\lambda _{o}}{\left ( 1 + \frac{eE_{o}}{mv_{o}}t \right )}

  4. \lambda_{o}

Virohan Allied & Healthcare Programs

Allied & Healthcare programs | 20+ Partner Universities & Institutes | 98% placement record

Apply

Solution

F=-e(-E_0\hat{i})=eE_0\hat{i}

a=eE_0\hat{i}/m

(\text{Acceleration is uniform, so from v=u+at})

At time t the magnitude of the velocity

v=v_{0}+\frac{eE_{0}}{m}t

Momentum

p(t)=m(v_{0}+ \frac{eE_{0}t}{m})

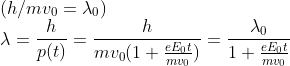
\\(h/mv_0=\lambda_0)\\\lambda = \frac{h}{p(t)} = \frac{h}{mv_{0}(1+ \frac{eE_{0}t}{mv_{0}})}=\frac{\lambda _{0}}{1+\frac{eE_{0}t}{mv_{0}}}\

So option C is the right answer.

Q.6 NEET - 2019

An electron is accelerated through a potential difference of 10000 V . Its de Broglie wavelength is

( m_ e ) = 9 \times 10 ^{-31} Kg

Solution

Use the equation-

\lambda _{e }= \frac{12.27}{\sqrt{V}}A^{\circ}

\lambda _{electron}= \frac{12.27}{\sqrt{10^4}}A^{\circ}=12.27*10^{-12}m

In the last 5 years’ (2017-2021) NEET papers, 9 questions were asked and out of these 6 were from the topics de Broglie Wavelength and Einstein's Photoelectric Equation. That is, 66.67% of questions from Dual Nature were from these two topics.

Recommended eBooks

Related eBooks & Sample Papers

Articles
Related Stories
|
Upcoming Medicine Exams
Karnataka Common Entrance Test for BSc Nursing
Ongoing Dates
KCET BSc Nursing Application Date

17 Jan'26 - 27 Feb'26 (Online)

Maharashtra Bachelor of Science in Nursing Common Entrance Test
Ongoing Dates
MH BSc Nursing CET Application Date

24 Jan'26 - 24 Feb'26 (Online)

Odisha BSc Nursing
Ongoing Dates
Odisha BSc Nursing Application Date

28 Jan'26 - 22 Mar'26 (Online)

Certifications By Top Providers
Biomolecules Structure Function in Health and Disease
Via All India Institute of Medical Sciences New Delhi
Industrial Biotechnology
Via Indian Institute of Technology Kharagpur
Certificate Course in Biostatistics, Epidemiology and Research Methodology
Via Manipal Academy of Higher Education, Manipal
Nutrition in the Health Sector
Via The University of Adelaide, Adelaide
Pathology
Via Tsinghua University, Beijing
Online M.Sc Psychology
Via Centre for Distance and Online Education, Andhra University
Coursera
 355 courses
Futurelearn
 310 courses
Edx
 233 courses
Udemy
 191 courses
Swayam
 106 courses
Explore Top Universities Across Globe
University College London, London
Gower Street, London, WC1E 6BT
University of Essex, Colchester
Wivenhoe Park Colchester CO4 3SQ
University of Nottingham, Nottingham
University Park, Nottingham NG7 2RD
University of Wisconsin, Madison
329 Union South 1308 W. Dayton Street Madison, WI 53715-1149
University of Alberta, Edmonton
116 St. and 85 Ave., Edmonton, Alberta, Canada T6G 2R3
Keele University, Newcastle
Staffordshire, UK, ST5 5BG

Popular Courses and Specializations

Popular Degrees

Popular Branches

List of colleges accepting NEET

Questions related to NEET

On Question asked by student community

Have a question related to NEET ?
I want free mock test for Neet 2026

Hi Gawade,
please refer to this article - https://medicine.careers360.com/articles/neet-ug-mock-tests

You can find the mock test link here

Read Complete Answer
R
Ritika Jonwal
9 Feb'26
My rank is 5000 on neet-ug, which college would be better for me?

Government Medical Colleges in states like Rajasthan, Uttar Pradesh, Madhya Pradesh, Bihar, Haryana, Punjab, Gujarat, Maharashtra

Read Complete Answer
K
Krishan Saini
28 Jan'26
Most important chapters with concepts neet for 2027 hindi midium 11 class

Hi Arti,

Please refer to these links

Weightage:

https://medicine.careers360.com/articles/neet-biology-chapter-wise-weightage

High-weightage chapters:

https://medicine.careers360.com/articles/neet-2026-high-weightage-chapters

Do or Die Biology:

https://medicine.careers360.com/articles/do-or-die-chapters-in-biology-for-neet

Hindi syllabus:

https://medicine.careers360.com/hi/articles/neet-syllabus

Most Scoring Concepts eBook (free PDF):

https://medicine.careers360.com/download/ebooks/neet-most-scoring-chapters-topics-based-on-past-5-year-analysis


Read Complete Answer
R
Ritika Jonwal
13 Feb'26
I have left 3 months for neet 2026 in which I have to test nd everything,I took drop this year evn though I studied in that period but not revised that's why it's getting hard for me now nd my physical nd chem isn't strong Bio is still fine what should I do now

You still have enough time. For NEET 2026 (drop year, 3 months left), focus on:

NCERT linebyline for highweightage chapters (Human Physiology, Plant Physiology, Cell, Biomolecules, Biological Classification, Plant/Animal Kingdom, Genetics, Ecology)

Daily chapterwise MCQs + PYQs and weekly full mocks with proper analysis

Useful Careers360 links for planning:

NEET

Read Complete Answer
A
avinash.dongre
9 Feb'26
Kya open category bhi neet de sakte hai is it is free

Yes, open category students can also appear in the NEET exam. Candidates must check the detailed eligibility criteria in the NEET information brochure. Applicants from the open category have to pay the NEET form fees for Rs. 1700.

Read Complete Answer
U
Ujjwal Kirti
19 Feb'26
View all

Popular NEET Questions

Column I ( Salivary gland)

 

Column II ( Their location)

Parotids

I

Below tongue

Sub-maxillary / sub-mandibular

Ii

Lower jaw

Sub-linguals

Iii

Cheek
Option: 1

a(i), b(ii) , c(iii)

 


Option: 2

a(ii), b(i), c(iii)

 


Option: 3

a(i), b(iii), c(ii)


Option: 4

a(iii), b(ii), c(i)


Read Complete Answer

Ethyl \; ester \xrightarrow[(excess)]{CH_{3}MgBr} P

the product 'P' will be ,

Option: 1


Option: 2


Option: 3

\left ( C_{2}H_{5} \right )_{3} - C- OH


Option: 4


Read Complete Answer

 

    

           

 Valve name                            

              

Function
    I   Aortic valve     A

Prevents blood from going backward from the pulmonary artery to the right ventricle.
    II   Mitral valve     B

 Prevent blood from flowing backward from the right ventricle to the right atrium.
    III   Pulmonic valve     C

 Prevents backward flow from the aorta into the left ventricle.
    IV   Tricuspid valve     D

 Prevent backward flow from the left ventricle to the left atrium.

 

Option: 1

I – A , II – B, III – C, IV – D


Option: 2

 I – B , II – C , III – A , IV – D


Option: 3

 I – C , II – D , III – A , IV – B


Option: 4

 I – D , II – A , III – B , IV – C 

 

 


Read Complete Answer

Column A Column B
A

a) Organisation of cellular contents and further cell growth.  
B

b) Leads to formation of two daughter cells.
C

c) Cell grows physically and increase volume proteins,organells.
D

d)  synthesis and replication of DNA.

Match the correct option as per the process shown in the diagram. 

 

 

 

Option: 1

1-b,2-a,3-d,4-c
 


Option: 2

1-c,2-b,3-a,4-d


Option: 3

1-a,2-d,3-c,4-b

 


Option: 4

1-c,2-d,3-a,4-b


Read Complete Answer

0.014 Kg of N2 gas at 27 0C is kept in a closed vessel. How much heat is required to double the rms speed of the N2 molecules?

Option: 1

3000 cal


Option: 2

2250 cal


Option: 3

2500 cal


Option: 4

3500 cal


Read Complete Answer

0.16 g of dibasic acid required 25 ml of decinormal NaOH solution for complete neutralisation. The modecular weight of the acid will be

Option: 1

32


Option: 2

64


Option: 3

128


Option: 4

256


Read Complete Answer

0.5 F of electricity is passed through 500 mL of copper sulphate solution. The amount of copper (in g) which can be deposited will be:

Option: 1

31.75


Option: 2

15.8


Option: 3

47.4


Option: 4

63.5


Read Complete Answer

0.5 g of an organic substance was kjeldahlised and the ammonia released was neutralised by 100 ml 0.1 M HCl. Percentage of nitrogen in the compound is

Option: 1

14


Option: 2

42


Option: 3

28


Option: 4

72


Read Complete Answer

0xone is

Option: 1

\mathrm{KO}_{2}


Option: 2

\mathrm{Na}_{2} \mathrm{O}_{2}


Option: 3

\mathrm{Li}_{2} \mathrm{O}


Option: 4

\mathrm{CaO}


Read Complete Answer

(1) A substance  known as "Smack"

(2) Diacetylmorphine

(3) Possessing a white color

(4) Devoid of any odor

(5) Crystal compound with a bitter taste

(6) Obtained by extracting from the latex of the poppy plant

The above statements/information are correct for:

Option: 1

Morphine


Option: 2

Heroin


Option: 3

Cocaine


Option: 4

Barbiturates


Read Complete Answer

Begin a career in Medical and Allied Sciences. Admissions Open for

Virohan Allied & Healthcare Programs
Apply

Allied & Healthcare programs | 20+ Partner Universities & Institutes | 98% placement record

Apollo Healthcare Academy
Apply

Get Job-Ready with New-Age Allied Health Programmes

Emversity Allied Health Programs
Apply

Get Job Ready in Healthcare | Employability-Focused Programs

Amity University-Noida Health and Allied Sciences Admissions
Apply

Amongst top 3% universities globally (QS Rankings) | Wide Range of scholarships available

SRM Kattankulathur Dental College Admissions 2026
Apply

Ranked #19 by NIRF, NAAC A++ Accredited | Recognized by dental council of India

SRM Medical College Admissions 2026
Apply

Ranked #18 by NIRF, NAAC A++ Accredited | Unmatched clinical exposure with over 7 lakh patients yearly

View all Application Forms

NEET Notifications

Latest updates

Explore Career Options

By Industry
Orthotist and Prosthetist

Orthotists and Prosthetists are professionals who provide aid to patients with disabilities. They fix them to artificial limbs (prosthetics) and help them to regain stability. There are times when people lose their limbs in an accident. In some other occasions, they are born without a limb or orthopaedic impairment. Orthotists and prosthetists play a crucial role in their lives with fixing them to assistive devices and provide mobility.

6 Jobs Available
Pathologist

A pathologist is required to examine body fluids, tissues, and organs with the help of laboratory tests and microscopic examinations. Pathologists often work in hospitals and diagnostic labs, often assisting doctors when it comes to treatment decisions. Due to the increased demand for diagnostic services, pathology offers good career opportunities in clinical practices, research and academics. 

5 Jobs Available
Veterinary Doctor

A Veterinarian is responsible for diagnosing, treating, and preventing diseases in animals. The individual performs surgeries, guides nutrition, and provides animal care. A Bachelor’s in Veterinary Science (B.Vsc.) is a mandatory degree. The profession brings together medical knowledge and a strong commitment to animal welfare. 

5 Jobs Available
Speech Therapist

A Speech Therapist (Speech-Language Pathologist) diagnoses and treats speech, language, communication, and swallowing disorders across all ages. They work in hospitals, schools, clinics, and more. Becoming an SLP requires a master’s degree, clinical training, and certification. With rising demand, the career offers rewarding opportunities in therapy, education, and research.

4 Jobs Available
Gynaecologist

A gynaecologist is a medical specialist in women’s reproductive health, handling issues like menstruation, fertility, pregnancy, and childbirth. They perform exams, surgeries, and offer family planning services. To become one, students must complete MBBS and postgraduate training. Gynaecologists work in hospitals or clinics and are in high demand, with salaries growing significantly with experience. 

4 Jobs Available
Audiologist

The audiologist career involves audiology professionals who are responsible to treat hearing loss and proactively preventing the relevant damage. Individuals who opt for a career as an audiologist use various testing strategies with the aim to determine if someone has a normal sensitivity to sounds or not. After the identification of hearing loss, a hearing doctor is required to determine which sections of the hearing are affected, to what extent they are affected, and where the wound causing the hearing loss is found. As soon as the hearing loss is identified, the patients are provided with recommendations for interventions and rehabilitation such as hearing aids, cochlear implants, and appropriate medical referrals. While audiology is a branch of science that studies and researches hearing, balance, and related disorders.

3 Jobs Available
Oncologist

An oncologist is a medical doctor who diagnoses and treats cancer using chemotherapy, radiation, surgery, and other therapies. They work with a team to create treatment plans tailored to each patient. Specialisations include medical, surgical, radiation, pediatric, gynecologic, and hematologic oncology. Becoming an oncologist in India requires an MBBS and postgraduate studies in oncology.

3 Jobs Available
Biochemist

A biochemist studies the chemical processes within living organisms, combining chemistry and biology. They conduct experiments, analyse data, and develop products like drugs and vaccines. Biochemists work in labs, healthcare, research, and education. A degree in biochemistry or related fields is essential, with advanced roles often requiring higher degrees. They also ensure quality control and may teach or mentor others.

2 Jobs Available

Never miss NEET update

Get timely NEET updates directly to your inbox. Stay informed!